Допустим, что функция 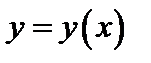 задана неявно уравнением
задана неявно уравнением
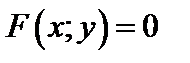 (18.12)
(18.12)
и требуется найти 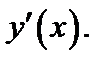
1-й способ. Если практически возможно, из (18.12) выражают явно 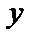 через
через 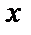 и дифференцируют.
и дифференцируют.
2-й способ. Дифференцируют уравнение (18.12), считая 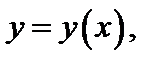 и выражают затем
и выражают затем 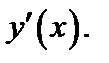
3-й способ. Используют формулу
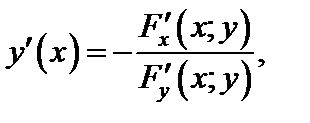 (18.13)
(18.13)
если 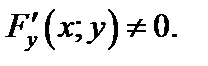
Способы 1–2 были рассмотрены в теории дифференцирования функции одной переменной и не всегда являются рациональными.
Производные неявной функции 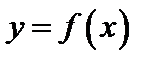 порядка выше первого находят последовательным дифференцированием формулы (18.13), учитывая, что y – функция от x.
порядка выше первого находят последовательным дифференцированием формулы (18.13), учитывая, что y – функция от x.
Для нахождения частных производных функции 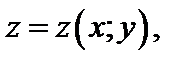 заданной неявно уравнением
заданной неявно уравнением
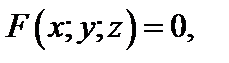 (18.14)
(18.14)
используют формулы
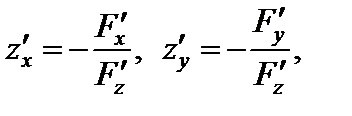 (18.15)
(18.15)
при условии, что эти производные существуют и 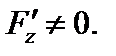
 2015-04-20
2015-04-20 654
654








