2015-04-20
390
Дифференциал второго порядка функции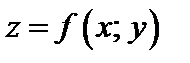 
определяется формулой
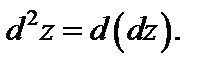(18.25)
Аналогично определяются дифференциалы третьего и высших порядков.
Справедлива формула
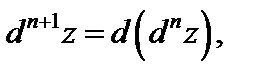
(18.26)
Если функция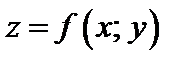 
имеет непрерывные частные производные, и переменные х и у являются независимыми, то дифференциалы второго и третьего порядков вычисляются по формулам:
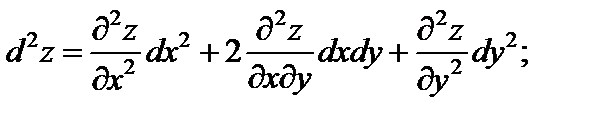(18.27)
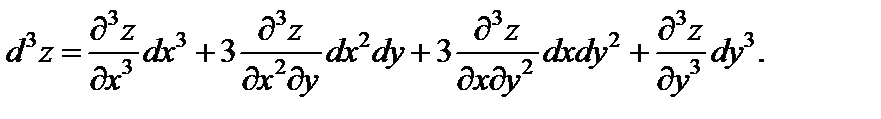(18.28)
Для всякого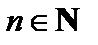 
формула вычисления дифференциала порядка 
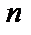по форме записи аналогична формуле бинома Ньютона:
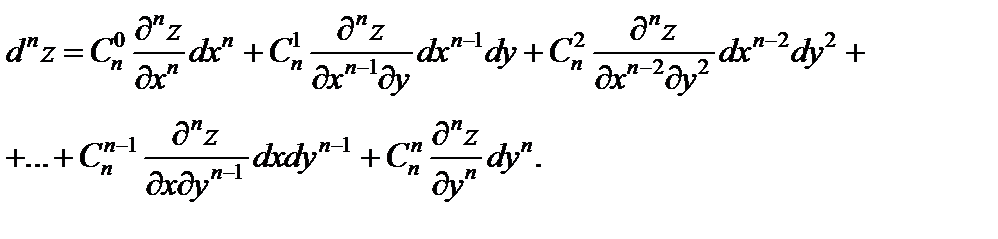(18.29)
Формула Тейлора для функции нескольких переменных.
