2015-04-20
358
Пусть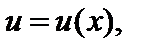 
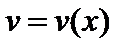– дифференцируемые функции на некотором множестве 
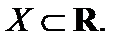Тогда:
1) 
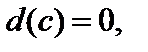
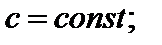
2) 
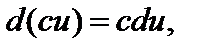
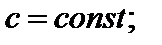
3) 
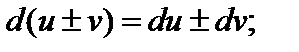
4) 
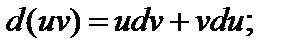
5) 
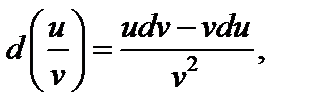
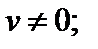
6) 
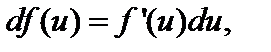где f (u) – сложная функция, дифференцируемая по переменной 
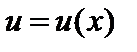(свойство инвариантности дифференциала), т. е.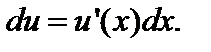 
При достаточно малом значении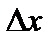 
приращение функции с большой степенью точности можно заменить дифференциалом функции:
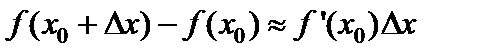или
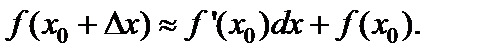(17.11)
С геометрической точки зрения дифференциал функции dy равен приращению ординаты касательной к кривой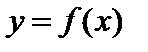 
в точке 
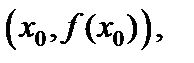когда аргумент получает приращение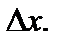 
Полные дифференциалы. Частные дифференциалы.
