2015-04-20
691
Пусть поверхность задана уравнением
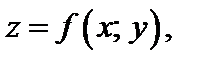
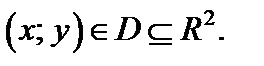
Тогда уравнение касательной плоскости в точке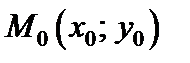 
имеет вид:
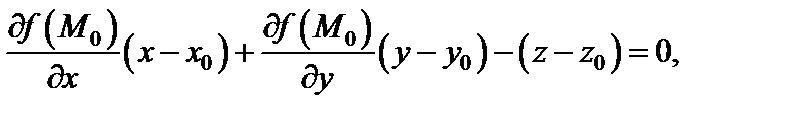(18.16)
где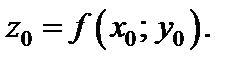 
Нормалью к поверхности в точке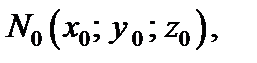 
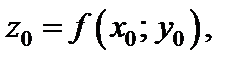называется прямая, проходящая через точку 
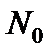перпендикулярно к касательной плоскости в этой точке.
Уравнение нормали к поверхности (18.16) в точке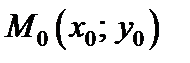 
имеет вид:
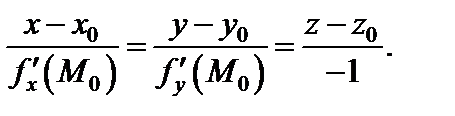(18.17)
Если поверхность задана уравнением
(18.18)
и в точке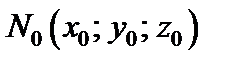 
этой поверхности существуют частные производные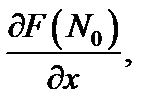 
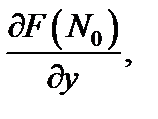
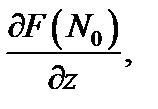не равные нулю одновременно, то уравнение касательной плоскости к поверхности (18.18) в точке 
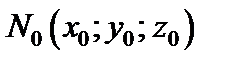имеет вид:
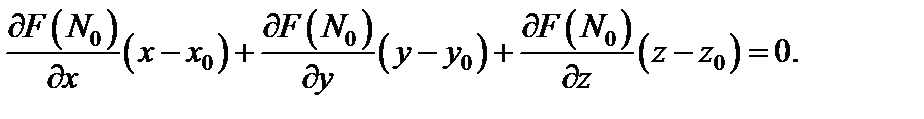(18.19)
Уравнение нормали к поверхности (18.18) в точке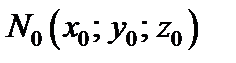 
имеет вид:
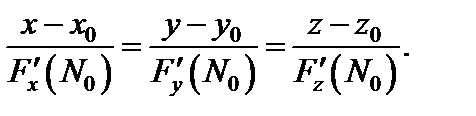(18.20)
