Функция 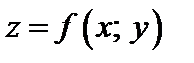 имеет в точке
имеет в точке 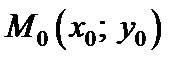 локальный максимум (минимум), если существует такая d -окрестность точки М 0, что для всех точек
локальный максимум (минимум), если существует такая d -окрестность точки М 0, что для всех точек 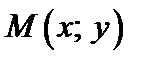 из этой окрестности (отличных от М 0) выполняется неравенство
из этой окрестности (отличных от М 0) выполняется неравенство
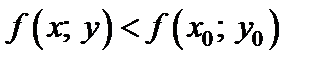
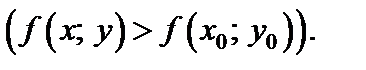
Максимум и минимум функции называются ее экстремумами (локальными), а точка М 0, в которой достигается экстремум, называется точкой экстремума.
Достаточное условие экстремума. Пусть 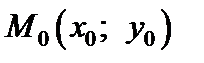 – стационарная точка дважды непрерывно дифференцируемой функции
– стационарная точка дважды непрерывно дифференцируемой функции 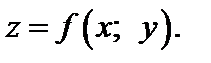 Обозначим:
Обозначим:
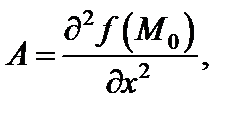
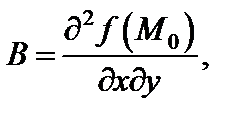
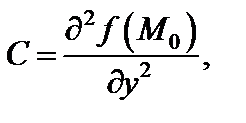
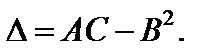
Тогда:
1) если 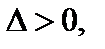 то функция имеет в точке М 0 локальный экстремум (максимум при
то функция имеет в точке М 0 локальный экстремум (максимум при 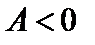 и минимум при
и минимум при 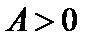 );
);
2) если 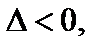 то в точке М 0 функция не имеет экстремума;
то в точке М 0 функция не имеет экстремума;
3) если 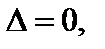 то в точке М 0 функция может иметь локальный экстремум, а может и не иметь его (нужны дополнительные исследования).
то в точке М 0 функция может иметь локальный экстремум, а может и не иметь его (нужны дополнительные исследования).
Допустим, что функция f (x; y) определена на некотором множестве 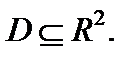
Число С называют наибольшим значением функции (глобальный максимум) на множестве D, если
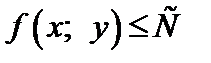
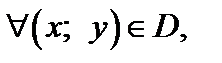 записывают так:
записывают так:
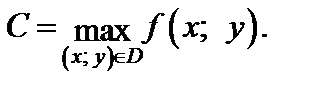
Число с называют наименьшим значением функции (глобальным минимумом) на множестве D, если
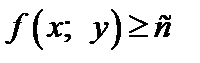
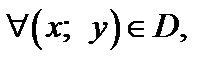 записывают так:
записывают так:
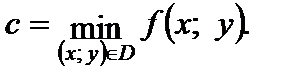
 2015-04-20
2015-04-20 653
653








