Производной функции 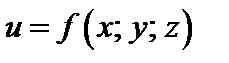 в точке
в точке 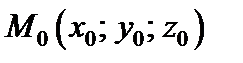 по направлению
по направлению 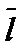 называется предел
называется предел
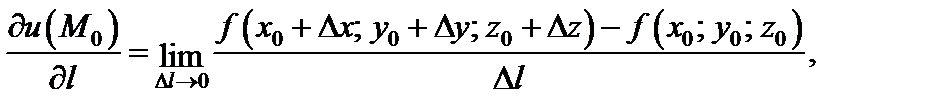
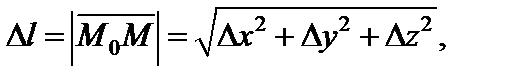
если предел существует.
Если функция 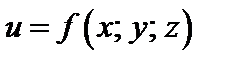 дифференцируема, то производная по направлению вычисляется по формуле
дифференцируема, то производная по направлению вычисляется по формуле
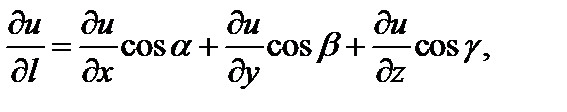 (18.31)
(18.31)
В частности, если 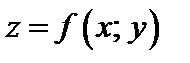 – функция двух переменных, то формула (18.31) производной по направлению примет вид:
– функция двух переменных, то формула (18.31) производной по направлению примет вид:
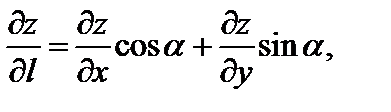 (18.32)
(18.32)
где 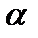 – угол между вектором
– угол между вектором 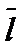 и осью Ох.
и осью Ох.
Градиентом функции 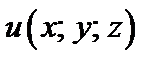 в точке
в точке 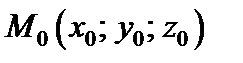 называется вектор
называется вектор
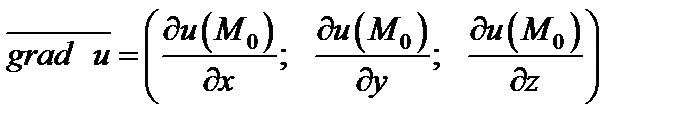 (18.33)
(18.33)
или, то же самое,
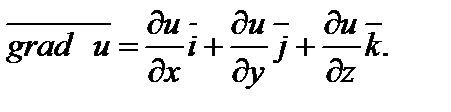
Связь между градиентом функции и производной по направлению устанавливает формула
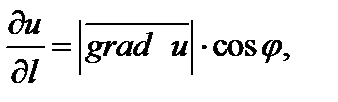
где 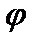 – угол между векторами
– угол между векторами 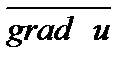 и
и 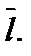
Градиент функции указывает направление наибыстрейшего возрастания функции. Наибольшее значение производной 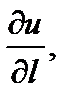 достигаемое в направление градиента, равно
достигаемое в направление градиента, равно
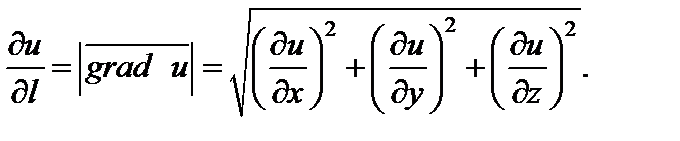
В частности, если 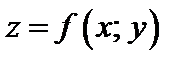 – функция двух переменных, то
– функция двух переменных, то
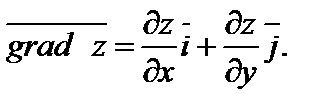
 2015-04-20
2015-04-20 440
440








