Предел последовательности. Число а называется пределом последовательности, если для любого положительного числа Е найдется такое натуральное число N

Число а называется пределом последовательности, если для любого положительного числа Е найдется такое натуральное число N, что при всех n>N выполняется равенство:

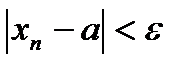. В этом случае пишут 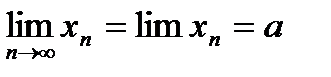и говорят, что последовательность {x_n}имеет предел, равный числу а. говорят,что последовательность сходится к а.

Коротко определение предела: .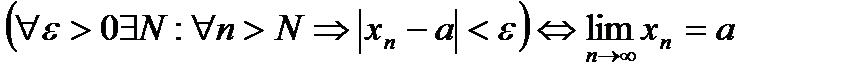

Сходящаяся последовательность имеет только один предел. Последовательность, неимеющая предела, называется расходящейся.

Если 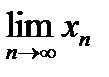=0 => последовательность бесконечно малая.

Если 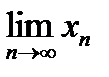= =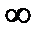> бесконечно большая.

=> .

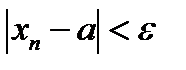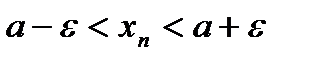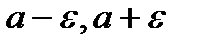- окрестности точки а.