Сформулируем два, эквивалентных между собой, определения предела функции в точке:
Определение (по Коши): число А называется пределом функции в точке х0, если для любого положительного 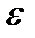 найдется такое положительное число
найдется такое положительное число 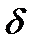 , что для всех х
, что для всех х 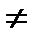 х0, удовлетворяющих неравенству
х0, удовлетворяющих неравенству 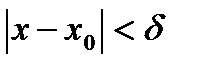 , выполняется неравенство
, выполняется неравенство 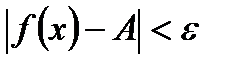 .
.
Коротко это определение:
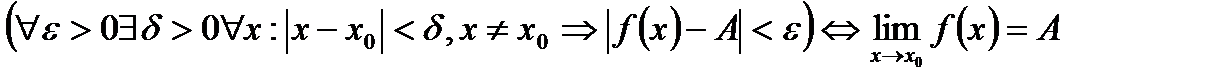 .
.
Определение (по Гейне):
Число А называется пределом функции 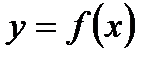 в точке х0, если для любой последовательности допустимых значений аргумента хn, сходящейся к х0, последовательность соответствующих значений функции
в точке х0, если для любой последовательности допустимых значений аргумента хn, сходящейся к х0, последовательность соответствующих значений функции 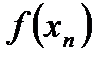 ,
, 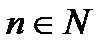 , сходится к числу А.
, сходится к числу А.
Односторонние пределы:
число А называется пределом функции 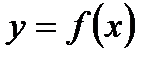 слева в точке x0, если для любого число
слева в точке x0, если для любого число 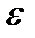 >0 существует число
>0 существует число 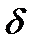 =
= 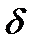 (
(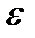 )>0 такое, что при
)>0 такое, что при 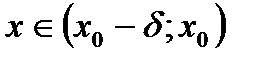 выполняется неравенство
выполняется неравенство 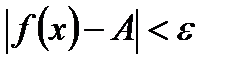 .
.
Предел слева записывают так: 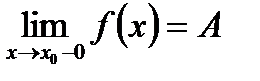
Аналогично определяется предел функции справа:
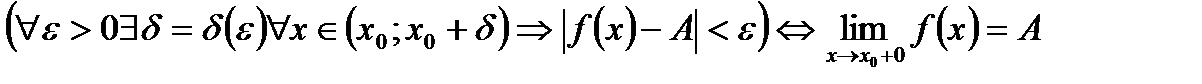 .
.
Пределы функции слева и справа называются односторонними пределами.
Предел функции при 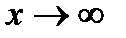 :
:
Число А называется пределом функции при 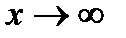 , если для любого положительного числа
, если для любого положительного числа 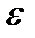 существует такое число М=М(
существует такое число М=М(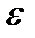 ) >0, что при всех х, удовлетворяющих неравенству
) >0, что при всех х, удовлетворяющих неравенству 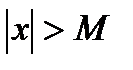 выполняется неравенство
выполняется неравенство 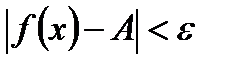 . Коротко:
. Коротко:
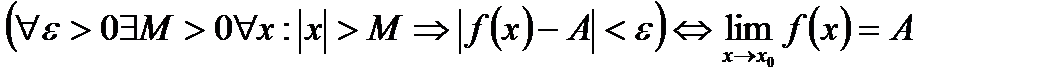
 2015-04-20
2015-04-20 553
553








