Дипольная пара. Нуль и полюс, расположенные близко друг к другу и к началу координат р-плоскости. Вводятся в систему с помощью интегрального корректирующего звена с целью повышения коэффициента усиления.
Доминирующие полюса. Полюса системы, оказывающие наибольшее влияние на динамику переходного процесса.
Корректирующее устройство. Элемент или схема, дополнительно вводимые в систему с целью улучшения ее качеств.
ПИ-регулятор (пропорционально-интегральный). Регулятор, содержащий два параллельные каналы: один канал формирует сигнал, пропорциональный ошибке системы, другой канал формирует сигнал, пропорциональных интеграла от ошибки. Выходной сигнал регулятора равен их сумме.
Синтез систем управления. Многоэтапная процедура, связанная с выбором структуры системы и определением входящих в нее элементов и их параметров. При этом часто приходится искать компромисс между несколькими конфликтующими критериями синтеза системы.
Глава 10. Статистические задачи линейных систем автоматического управления
Методы расчета систем, подверженных случайным воздействиям, составляют в теории управления отдельную ветвь, называемую Статистической динамикой (СД).
Теоретические основы СД созданы Н. Винером, А.Н. Колмогоровым, А.Я. Хинчиным, а также В.С. Пугачевым и В.В. Солодовниковым.
Различают в СД три типа задач расчета автоматических систем:
- Определение Статистических характеристик выходных сигналов (управляемой величины или сигнала ошибки) при полностью заданной структуре системы, заданных параметрах объекта и управляющего устройства и известных характеристиках внешних воздействий.
- При полностью заданных структуре системы, заданных параметрах объекта управления и известных Статистических характеристиках воздействий необходимо так выбрать параметры системы, чтобы получить минимум среднеквадратичной ошибки (минимум дисперсии ошибки).
- При заданных вероятностных характеристиках полезного сигнала и помехи необходимо определить оптимальную структуру и параметры системы (или только управляющего устройства), при которых обеспечивается получение теоретического минимума среднеквадратичной ошибки. Это так называемая “задача Винера” (решаются уравнения Винера-Хопфа и Винера-Колмогорова).
Задача Винера Н. формулируется как задача синтеза структуры линейной системы по критерию минимума дисперсии при стационарных случайных воздействиях.
10.1 Задача первого типа

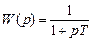
u – “белый шум”
Найти среднеквадратичное значение помехи на выходе звена:
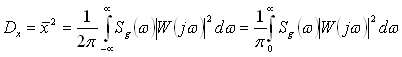
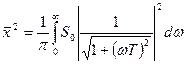
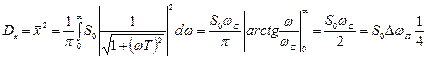
 Т.о. среднеквадратичное значение помехи (“шума”) на выходе звена пропорционально полосе пропускания. Следовательно возникает противоречие между быстродействием и шумами.
Т.о. среднеквадратичное значение помехи (“шума”) на выходе звена пропорционально полосе пропускания. Следовательно возникает противоречие между быстродействием и шумами.
Длительность переходного процесса тем меньше (быстродействие выше), чем шире полоса пропускания, но чем шире полоса пропускания, тем выше уровень шумов.
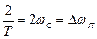 – ширина полосы пропускания
– ширина полосы пропускания
Примером такого источника “белого” шума могут быть тепловые шумы сопротивления, которые дают уровень спектральной плотности хаотичного напряжения на этом сопротивлении 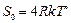 , где
, где
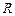 – сопротивление,
– сопротивление,
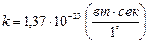 – постоянная Больцмана,
– постоянная Больцмана,
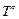 – абсолютная температура.
– абсолютная температура.
10.2 Задача второго типа
Дана структурная (алгоритмическая) схема замкнутой системы:
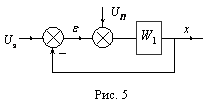
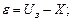
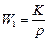 ,
, 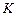 – передаточный коэффициент,
– передаточный коэффициент, 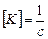 (иногда
(иногда 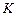 – добротность по скорости)
– добротность по скорости)
Надо определить оптимальное значение 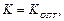 при котором суммарная дисперсия (разброс) сигнала рассогласования
при котором суммарная дисперсия (разброс) сигнала рассогласования 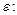
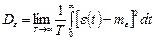 минимальна;
минимальна;
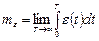 – математическое ожидание (среднее значение) сигнала
– математическое ожидание (среднее значение) сигнала 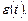
Дисперсия является мерой разброса мгновенных значений сигнала около математического ожидания. Чем больше пульсация переменной составляющей сигнала около его постоянной составляющей, тем больше дисперсия сигнала. Дисперсия имеет размерность величины 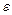 в квадрате.
в квадрате.
 Часто в качестве меры разброса случайного сигнала используют среднеквадратичное отклонение:
Часто в качестве меры разброса случайного сигнала используют среднеквадратичное отклонение:
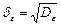
На входе системы действует задающее воздействие 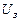 , которое характеризуется экспоненциальной корреляционной функцией:
, которое характеризуется экспоненциальной корреляционной функцией: 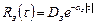
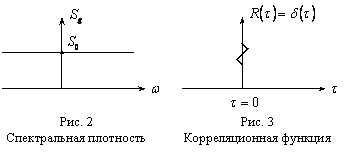
и спектральной плотностью:
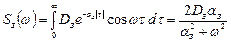
 Чем больше
Чем больше 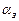 , тем “острее” график корреляционной функции и шире график спектральной плотности.
, тем “острее” график корреляционной функции и шире график спектральной плотности.
На входе системы также действует помеха 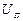 в виде “белого шума” со спектральной плотностью
в виде “белого шума” со спектральной плотностью
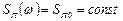 при
при 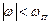 ,
, 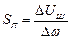 ,
, 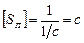
причем 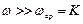

Передаточная функция, связывающая 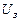 и
и 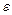 :
:
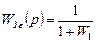
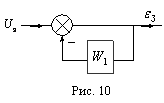
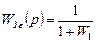
Комплексный коэффициент передачи (ККП) или “частотная функция”:
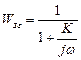
Передаточная функция и ККП, связывающие 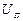 и
и 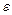 :
:
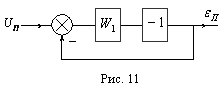
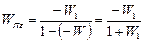
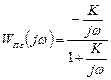
Если внешние воздействия 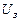 и
и 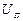 не коррелированны между собой, то сигнал ошибки
не коррелированны между собой, то сигнал ошибки 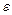 , возникающий в системе, может рассматриваться как сумма двух независимых составляющих
, возникающий в системе, может рассматриваться как сумма двух независимых составляющих
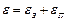
Составляющая 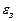 обусловлена неточным воспроизведением задающего воздействия, а составляющая
обусловлена неточным воспроизведением задающего воздействия, а составляющая 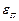 – неполным подавлением возмущения
– неполным подавлением возмущения 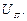
Для определения дисперсии сигналов на выходе 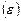 системы практически удобно пользоваться соотношениями в частной области.
системы практически удобно пользоваться соотношениями в частной области.
Дисперсия, обусловленная неточным воспроизведением задающего воздействия 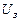 :
:
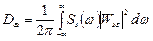 (1)
(1)
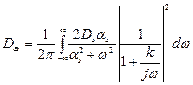 (2)
(2)
Из (2) видно, что при подстановке в общее соотношение (1) конкретных функций 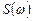 и
и 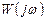 получаются довольно сложные выражения, интегрирование которых обычными методами затруднительно. Поэтому используют методику аналогичную методике для вычисления квадратичных интегральных оценок (формулы Парсеваля). В соответствии с этой методикой дисперсию определяют по формуле:
получаются довольно сложные выражения, интегрирование которых обычными методами затруднительно. Поэтому используют методику аналогичную методике для вычисления квадратичных интегральных оценок (формулы Парсеваля). В соответствии с этой методикой дисперсию определяют по формуле:
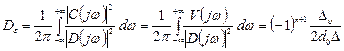
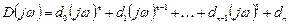
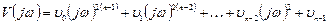
Для простейших случаев:
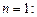
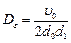
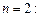
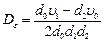
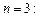
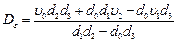
При этом для получения коэффициентов полинома 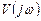 следует вначале найти квадрат модуля полинома
следует вначале найти квадрат модуля полинома 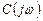 , а затем все слагаемые с четными степенями
, а затем все слагаемые с четными степенями 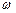 привести к виду с нечетными степенями
привести к виду с нечетными степенями 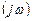 , поменяв при необходимости знаки слагаемых, т.е. записать
, поменяв при необходимости знаки слагаемых, т.е. записать 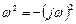 .
.
Итак, преобразуем (2):
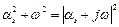
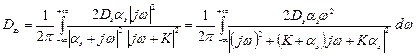
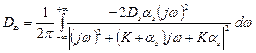
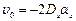 ;
; 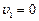
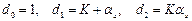
Следовательно,
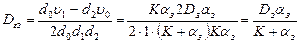
Чем больше K, тем меньше дисперсия 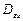 , т.е. тем точнее система воспроизводит на выходе задающее воздействие.
, т.е. тем точнее система воспроизводит на выходе задающее воздействие.
Дисперсия, обусловленная влиянием помехи 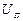 :
:
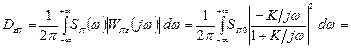
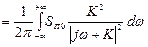
Значение 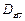 при
при 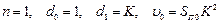 примет вид:
примет вид:
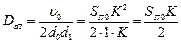
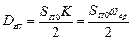
Чем больше коэффициент K, тем больше ошибка из-за прохождения помехи 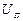 на выход системы.
на выход системы.
Суммарная дисперсия сигнала ошибки:
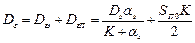
Значение K, обеспечивающее минимальную дисперсию (разброс) найдем из условия:
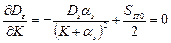
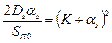
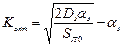
Графики зависимости дисперсий сигнала ошибки в зависимости от передаточного коэффициента 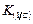 разомкнутой системы даны на рисунке:
разомкнутой системы даны на рисунке:
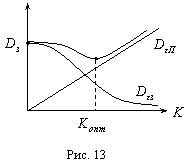
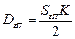
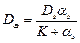
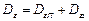
Например, если 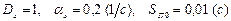 , то
, то
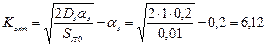
Видно, что 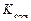 зависит только от параметров внешних воздействий. В частности, чем больше параметр
зависит только от параметров внешних воздействий. В частности, чем больше параметр 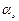 , тем быстрее уменьшается корреляционная функция, тем ближе сигнал к чисто случайному и тем шире график спектральной плотности.
, тем быстрее уменьшается корреляционная функция, тем ближе сигнал к чисто случайному и тем шире график спектральной плотности.

При 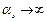 рассматриваемый сигнал приближается к идеальному “белому шуму”.
рассматриваемый сигнал приближается к идеальному “белому шуму”.
10.3 Задача третьего типа
Определение оптимальной (по минимуму дисперсии) передаточной функции системы управления.
Назначение любой системы управления изменять входную величину 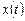 по определенному закону и устранять влияние возмущений на эту величину. В общем случае автоматическая система должна воспроизводить на своем выходе не само воздействие
по определенному закону и устранять влияние возмущений на эту величину. В общем случае автоматическая система должна воспроизводить на своем выходе не само воздействие 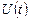 , а некоторый требуемый сигнал
, а некоторый требуемый сигнал 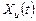 (идеальный сигнал), связанный с сигналом
(идеальный сигнал), связанный с сигналом 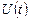 заданным соотношением:
заданным соотношением:
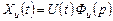 , где
, где
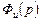 – заданный оператор идеального преобразования входного сигнала. Если система выполняет операцию идеально и ее выходная величина
– заданный оператор идеального преобразования входного сигнала. Если система выполняет операцию идеально и ее выходная величина 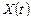 соответствует требуемому значению, то можно написать:
соответствует требуемому значению, то можно написать:
для слежения: 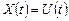 ;
; 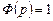 (если обратная связь
(если обратная связь 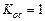 )
)
или 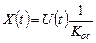 (если
(если 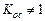 )
)
для дифференцирования: 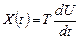
для упреждения: 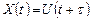 и т.д.
и т.д.
Сигнал 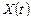 на выходе реальной системы
на выходе реальной системы 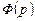 почти всегда отличается от идеального выходного сигнала на величину ошибки
почти всегда отличается от идеального выходного сигнала на величину ошибки
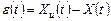
В связи с этим возникает задача синтеза такой структуры, которая обеспечивала бы наилучшее в том или ином смысле, приближение к идеальному преобразованию 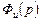 . Критерием точности приближения реальной структуры к идеальной может служить условие минимума дисперсии сигнала ошибки. Это и есть задача Винера.
. Критерием точности приближения реальной структуры к идеальной может служить условие минимума дисперсии сигнала ошибки. Это и есть задача Винера.
Рассмотрим упрощенное решение задачи Винера применительно к расчетной схеме:
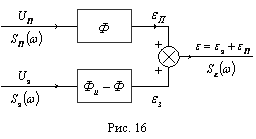
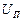 – помеха на входе
– помеха на входе
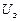 – задающий сигнал
– задающий сигнал
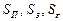 – соответствующие спектральные плотности.
– соответствующие спектральные плотности.
Полагаем, что входные воздействия 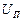 и
и 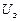 не коррелированны между собой. Поэтому спектральную плотность сигнала
не коррелированны между собой. Поэтому спектральную плотность сигнала 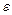 можно определить как простую сумму:
можно определить как простую сумму:
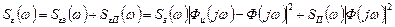
Дисперсия сигнала ошибки:
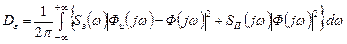 (*)
(*)
Задача Винера заключается в определении такой частотной передаточной функции (иначе ККП) 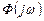 замкнутой системы, которая обеспечивает минимум дисперсии
замкнутой системы, которая обеспечивает минимум дисперсии 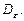 После преобразований (*) принимает вид:
После преобразований (*) принимает вид:
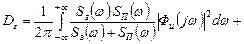
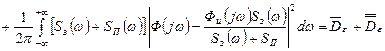
Это уравнение Винера Хопфа.
В первое слагаемое не входит 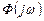 и на него нельзя повлиять выбором
и на него нельзя повлиять выбором 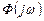 . Очевидно, условием минимума
. Очевидно, условием минимума 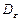 :
: 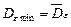 является равенство:
является равенство:
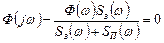
Следовательно,
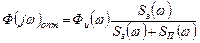 (**)
(**)
Т.о. 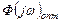 зависит от вида оператора идеального преобразования
зависит от вида оператора идеального преобразования 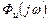 и соотношения спектральных плоскостей задающего воздействия и помехи.
и соотношения спектральных плоскостей задающего воздействия и помехи.
При отсутствии помехи 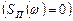 :
:
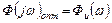
т.е. оптимальная частотная функция равна заданному оператору идеального преобразования.
Если помеха представляет “белый шум” и ее интенсивность 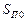 много больше уровня полезного сигнала
много больше уровня полезного сигнала 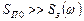 , то
, то
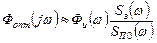
и для следящих систем 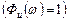 :
: 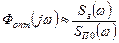
т.е. повторяет форму кривой спектральной плотности задания.
Однако частотные функции, определяемые (**), оказываются, как правило физически нереализуемыми. Это следует из того, что если найти весовую функцию 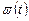 , соответствующую
, соответствующую 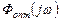 , то при
, то при 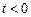 эта импульсная переходная функция будет отлична от 0, т.е.
эта импульсная переходная функция будет отлична от 0, т.е. 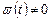 при
при 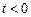 .
.
Это означает, что следствие (реакция на возмущение) предшествует причине (возмущению вида 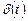 , приложенному в момент времени
, приложенному в момент времени 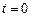 ).
).
Причина здесь в том, что частотная функция 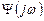 , соответствующая спектру
, соответствующая спектру 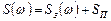 может иметь нули и полюса не только в левой полуплоскости
может иметь нули и полюса не только в левой полуплоскости 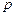 (верхней полуплоскости
(верхней полуплоскости 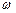 ), но и в правой полуплоскости
), но и в правой полуплоскости 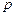 (нижней полуплоскости
(нижней полуплоскости 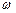 ).
).
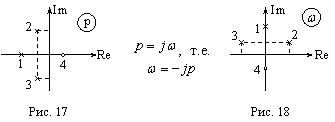
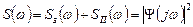
Для получения реализуемой оптимальной частотной характеристики 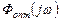 можно использовать операции факторизации и расщепления; для этого представим сумму спектральных плотностей в виде произведения двух сомножителей, один из которых
можно использовать операции факторизации и расщепления; для этого представим сумму спектральных плотностей в виде произведения двух сомножителей, один из которых 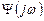 имеет нули и полюса в верхней полуплоскости
имеет нули и полюса в верхней полуплоскости 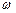 , а другой
, а другой 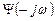 - в нижней.
- в нижней.
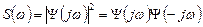
Тогда физически реализуемая частотная характеристика будет иметь вид:
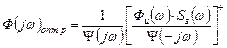 (***)
(***)
(***) – это уравнение Винера-Колмогорова, полученное в результате расщепления (отбрасывания в (**) нижних нулей и полюсов), имеет нули и полюса только в верхней полуплоскости 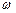 .
.
Пример:
Пусть спектральная плотность задающего сигнала
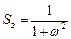
а спектральная плотность помехи (белый шум):
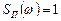
Задача состоит в построении следящей системы, т.е.
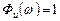
Для нахождения 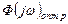 воспользуемся (*).
воспользуемся (*).
Произведем операцию факторизации:
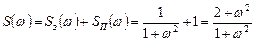
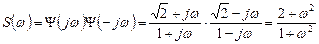
Затем произведем операцию расщепления:
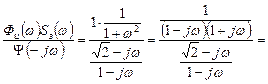
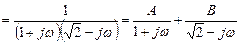
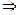
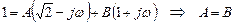
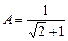
Таким образом, отбрасывая 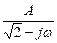 , имеющий нижний (в плоскости
, имеющий нижний (в плоскости 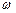 ) полюс
) полюс 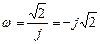 , получаем:
, получаем:
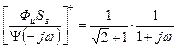
подставляя это значение 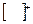 и
и 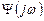 в (*), получаем:
в (*), получаем:
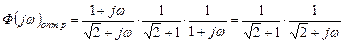
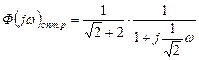 ,
,
что соответствует апериодическому звену со статическим коэффициентом усиления 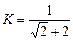 и постоянной времени
и постоянной времени 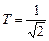 .
.
Подведем итоги:
Теоретический минимум дисперсии:
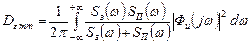
(Для нашего примера: 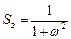 ;
; 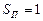 ;
; 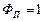 ):
):
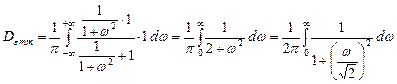
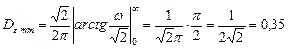
В физически реализуемой системе из-за различий функций 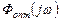 и
и 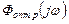 дисперсия возрастает на величину:
дисперсия возрастает на величину:
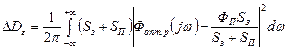
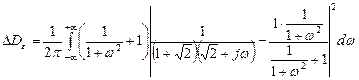
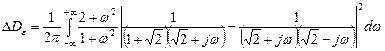
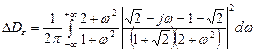
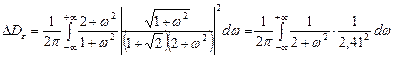
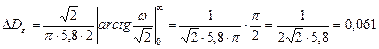
Итак, реально достижимое значение минимума дисперсии при 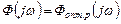 составит
составит 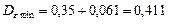
Ключевые термины и понятия.
Выбор некоторого параметра управляющего устройств, обеспечивающий минимальную дисперсию сигнала ошибки при известных характеристиках воздействий, заданной структуры системы, заданных параметрах объекта.
Выбор оптимальной структуры всей системы или только управляющего устройства при критерии в виде минимума дисперсии сигнала ошибки при известных характеристиках внешний воздействий (задача Винера).
Дисперсия стационарного случайного сигнала. Среднее значение квадрата отклонения сигнала от среднего значения (математического ожидания).
Статистическая динамика. Методы расчета систем, подверженных случайным воздействиям.
Тестовые вопросы и задачи на проверку минимальных знаний по курсу ТАУ:
1. Какие виды управления Вы знаете и чем они отличаются друг от друга?
2. Устойчива ли САУ 3-го порядка с приведенным годографом Михайлова
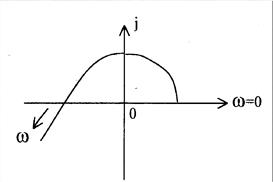
3. Оцените устойчивость линейной непрерывной системы 3-го порядка с данным расположением корней характеристического уровня.
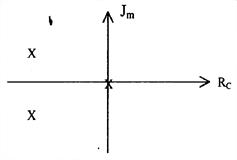
4. Найдите переходную функцию h (t) звена с передаточной функцией
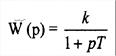
5. Сформулируйте необходимое условие устойчивости для линейных непрерывных систем.
6. Запишите передаточную функцию для идеального интегрирующего звена.
7. Устойчива ли система, если ее характеристическое уравнение имеет вид
Р4+ 5Р3 + ЗР+ 10 = 0
8. Что такое преобразование Лапласа и в чем его основное достоинство?
9. Найдите установившееся значение выходной величины:
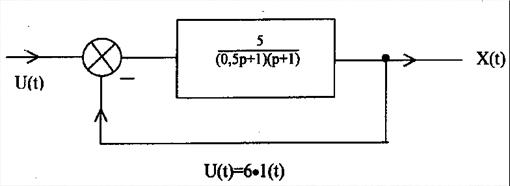
10. С какой целью в САР, построенную на основе принципа управления по отклонению, добавляют канал компенсации возмущающего воздействия?
11. Постройте асимптотическую ЛАЧХ звена с передаточной функцией
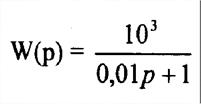
 2015-04-30
2015-04-30 1024
1024







