2015-04-20
1244
Комплексное число 
изображается на плоскости точкой или, эквивалентно, вектором с координатами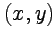 
(рис.1), и при таком способе задания операции сложения будет соответствовать векторное сложение. Плоскость называется комплексной плоскостью, ось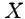 
- действительной осью и 
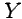- мнимой осью.
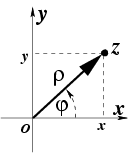
Рис.1.
В полярной системе координат на комплексной плоскости число будет определяться парой действительных чисел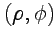 
(рис.1). Из уравнений, связывающих декартовую и полярную системы координат, следует:
|
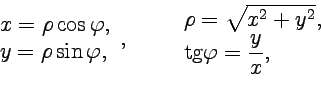и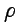 
имеет смысл модуля, а 
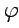называется аргументом числа , 
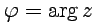. С использованием (8) число 
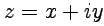запишется как
|
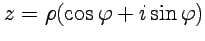и называется тригонометрической формой записи комлексного числа . Отметим, что аргумент определен с точностью до целого кратного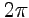 
, что записывается как
|
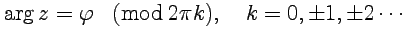Выражение в скобках формулы (9) может быть преобразовано с помощью соотношения:
|
которое называется формулой Эйлера и позволяет получить еще один способ записи комплексных чисел
|
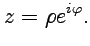Выражение (12) называется показательной формой записи комплексного числа и является одной из наиболее часто встречающихся в комплексном анализе. Использование символа экспоненты в (11) указывает на то, что эта величина должна обладать и теми же свойствами. Доказательство последнего утверждения будет удобнее рассмотреть на примере.
