Задание 1. Даны вершины треугольника АВС. Координаты точек A,B и C заданы в таблице. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0.01; 4) уравнение высоты CD и ее длину; 5) уравнение медианы АЕ и ее длину; 6) систему неравенств, определяющих треугольник АВС. Построить чертеж.
| № Вар-та | A | B | C | № Вар-та | A | B | C | № Вар-та | A | B | C |
| 1. | (-5;0) | (7;9) | (5;-5) | 2. | (-2;2) | (10;-7) | (8;7) | 3. | (-5;2) | (7;-7) | (5;7) |
| 4. | (-7;2) | (5;11) | (3;-3) | 5. | (1;2) | (13;-7) | (11;7) | 6. | (-7;5) | (5;-4) | (3;10) |
| 7. | (-5;-3) | (7;3) | (5;-8) | 8. | (-4;1) | (8;-8) | (6;6) | 9. | (-7;1) | (5;-8) | (3;6) |
| 10. | (-6;-2) | (6;7) | (4;-7) | 11. | (-7;-1) | (-5;-10) | (3;4) | 12. | (0;3) | (12;-6) | (10;8) |
| 13. | (-8;-4) | (4;5) | (2;-9) | 14. | (-3;3) | (9;-6) | (7;8) | 15. | (-8;4) | (4;-5) | (2;9) |
| 16. | (0;-1) | (12;8) | (10;-4) | 17. | (-2;1) | (10;10) | (8;-4) | 18. | (1;4) | (13;-5) | (11;9) |
| 19. | (-6;1) | (6;10) | (4;-4) | 20. | (-4;-1) | (8;8) | (6;-6) | 21. | (1;1) | (7;4) | (4;5) |
| 22. | (-2;-4) | (10;5) | (8;-9) | 23. | (-1;0) | (11;9) | (9;-3) | 24. | (1;1) | (-5;4) | (-2;5) |
| 25. | (-3;0) | (9;9) | (7;-5) | 26. | (-3;-3) | (9;6) | (7;-8) | 27. | (-1;1) | (5;4) | (2;5) |
| 28. | (-9;-2) | (3;7) | (1;-7) | 29. | (-3;0) | (9;9) | (7;-5) | 30. | (-1;1) | (-7;4) | (-4;5) |
Задание 2. Построить экономико-математическую модель задачи. Предприятие выпускает три вида продукции, используя сырье трех видов. Расходы сырья задаются матрицей A =(aij), где aij – это расход i-го сырья на 1ед. продукции j-го вида. Запасы сырья задаются матрицей Q=(qi), где qi – запас сырья i-го вида. Определить объем выпуска продукции каждого вида при заданных запасах сырья. Исходные данные приведены ниже в соответствующих таблицах (первые три столбца – матрица A, четвертый – матрица Q). Систему решить матричным способом.
| № вар-та | № вар-та | № вар-та | № вар-та | ||||
| 1. | 2 5 1 16 5 1 1 24 2 1 1 12 | 2. | 2 3 2 24 3 5 2 36 1 1 8 18 | 3. | 3 3 5 36 6 8 0 54 3 1 6 27 | 4. | 2 0 2 12 3 2 2 18 1 3 1 19 |
| 5. | 2 3 1 24 5 0 2 36 2 1 1 18 | 6. | 1 2 3 44 4 1 4 66 2 1 1 33 | 7. | 6 7 5 52 13 10 7 78 7 9 1 39 | 8. | 2 3 2 24 3 5 2 36 1 1 8 18 |
| 9. | 2 0 2 12 3 2 2 18 1 3 1 9 | 10. | 3 1 8 16 2 5 10 24 2 3 2 12 | 11. | 6 1 2 72 1 1 5 108 0 1 2 54 | 12. | 7 5 15 80 10 10 10 120 6 4 6 60 |
| 13. | 3 3 6 48 2 7 8 72 2 3 4 36 | 14. | 2 1 3 16 3 2 4 24 1 1 3 12 | 15. | 4 2 3 76 7 6 3 114 3 5 1 57 | 16. | 1 1 2 92 8 5 2 138 2 0 1 69 |
| 17. | 6 5 4 64 10 8 2 96 4 3 6 48 | 18. | 2 1 4 28 2 5 5 42 1 2 3 21 | 19. | 4 6 4 104 6 3 16 156 2 5 3 78 | 20. | 2 1 5 20 4 4 1 30 1 2 2 15 |
| 21. | 2 1 4 20 2 0 7 30 1 5 1 15 | 22. | 2 1 4 28 2 5 5 42 1 1 3 21 | 23. | 6 1 0 32 8 3 2 48 3 2 5 24 | 24. | 1 2 2 8 3 4 1 12 3 2 1 6 |
| 25. | 2 6 3 40 4 5 5 60 4 2 1 30 | 26. | 2 1 2 20 4 3 2 30 2 0 1 15 | 27. | 2 1 3 24 3 1 5 36 2 1 1 18 | 28. | 3 3 6 72 2 7 6 108 1 3 4 54 |
| 29. | 2 2 2 12 4 1 3 18 1 1 2 9 | 30. | 4 2 8 24 2 3 16 36 6 2 0 18 | 31. | 2 3 1 41 1 4 5 71 3 1 2 52 | 32. | 1 5 1 51 2 8 5 121 3 3 2 58 |
Задание 3. Исследовать (решить) 3 системы методом Гаусса (в таблицах даны элементы расширенных матриц систем 4-х уравнений с 4-мя неизвестными):
| № Вар-та | |
| 1. | 2 1 3 1 -1 2 1 -1 3 -8 2 1 -1 3 -8 1 -1 0 1 0 1 1 1 -2 -6 1 1 1 -2 2 5 7 -1 3 11 3 2 0 1 -14 3 2 0 1 -14 1 2 0 1 3 -1 3 1 -1 5 -1 3 1 -1 5 |
| 2. | 2 1 -1 3 14 5 -3 2 1 9 3 2 4 0 5 1 -1 4 -3 -11 1 -1 4 -3 -1 1 0 4 -1 1 3 2 0 1 14 2 -3 0 -3 2 2 2 0 1 3 -1 3 1 -1 4 3 0 2 4 7 3 1 -3 2 1 |
| 3. | 2 1 3 -1 7 3 2 4 0 4 2 1 3 3 7 1 -1 0 1 -1 1 0 4 -1 1 1 -1 0 4 -1 3 7 -1 3 48 2 2 0 1 3 2 -1 0 7 2 2 1 0 2 13 3 1 -3 2 1 1 0 0 3 1 |
| 4. | 5 -3 2 1 21 -3 0 1 2 -5 2 -1 3 1 8 1 -1 4 -3 -15 -3 1 3 1 2 1 2 3 -2 5 2 1 -3 1 30 4 -3 2 1 3 -1 1 2 -3 2 3 0 2 4 38 0 1 2 -1 7 0 3 5 -5 10 |
| 5. | 2 1 3 1 8 2 1 3 3 7 -1 1 0 2 2 1 -1 0 1 5 1 -1 0 4 -1 3 -2 1 4 4 3 7 -1 3 36 2 -1 0 7 0 2 -1 1 6 8 2 1 0 2 16 1 0 0 3 1 2 0 1 -1 -2 |
| 6. | 3 -1 1 4 45 2 -1 3 1 8 2 1 3 1 5 1 0 4 -1 -3 1 2 3 -2 5 2 1 -5 -1 2 2 2 0 1 18 -1 1 2 -3 2 4 2 -2 0 -6 3 1 -3 2 35 0 3 5 -5 7 3 -1 1 5 -2 |
| 7. | 5 -3 2 1 29 -1 1 0 2 2 1 4 6 -4 8 1 -1 4 -3 –19 3 -2 1 4 4 1 3 4 -3 9 2 -3 0 -3 -6 2 -1 1 6 6 0 1 2 -1 1 1 0 2 4 29 2 0 1 -1 -2 -1 -2 1 2 –14 |
| 8. | -3 0 1 2 -3 2 1 3 1 5 1 2 0 3 5 1 -1 -2 1 21 2 1 -5 -1 -11 -5 -3 1 -1 9 4 -3 2 1 45 4 2 -2 0 -6 -3 1 2 2 12 0 1 2 -1 -15 3 -1 1 5 -2 6 5 -1 4 -6 |
| 9. | 2 1 3 3 4 1 4 6 -4 10 -1 3 5 4 -8 1 -1 0 4 19 1 3 4 -3 9 1 -1 1 1 2 3 0 7 9 23 0 1 2 -1 1 1 -1 -2 1 -1 1 0 0 3 10 -1 -2 1 2 -14 1 -1 4 1 -7 |
| 10. | -3 1 1 2 -18 -1 3 5 4 -8 1 -1 4 1 -5 -3 1 3 1 -20 1 -1 1 1 -4 2 3 2 3 18 4 -3 2 1 24 1 -1 -2 1 -1 1 2 2 1 10 0 1 2 -1 -4 1 -1 4 1 -7 0 1 2 -1 0 |
| 11. | 2 -1 3 1 7 1 -1 4 1 -5 2 -5 3 -1 0 1 2 3 -2 2 2 3 2 3 18 3 -7 3 -1 2 -1 1 2 -3 -9 1 2 2 1 9 1 -9 6 7 3 2 -1 1 3 11 0 1 2 -1 0 4 -16 9 6 7 |
| 12. | -1 1 0 2 3 2 -5 3 -1 0 1 2 1 -1 10 3 -2 1 -4 -3 3 -7 3 -1 2 2 -1 1 0 -4 1 -1 3 -1 -4 1 -9 6 7 3 4 0 0 3 7 2 0 1 -1 5 4 -16 9 6 5 2 1 -1 3 7 |
| 13. | 2 1 3 1 17 1 3 2 3 1 1 20 1 -1 10 -1 1 1 3 7 2 8 2 8 0 2 -1 1 0 -4 4 2 -2 0 36 0 4 -1 2 1 4 0 0 3 8 3 -1 1 5 27 -2 -4 -3 -6 1 2 1 -1 3 7 |
| 14. | 1 1 1 0 9 3 -1 2 -5 11 3 -1 2 -5 10 1 3 4 -3 8 -1 1 0 1 -3 -1 1 0 1 -3 0 1 2 -1 1 4 -2 2 -6 14 4 -2 2 -6 14 -1 -2 1 2 -10 2 4 1 -1 -3 2 4 1 -1 -3 |
| 15. | 3 2 0 1 30 9 4 -5 2 -10 9 7 -5 2 -10 -5 -3 1 -1 -47 1 -1 3 -1 0 1 -1 3 -1 0 -3 1 2 2 -11 2 -3 0 1 0 4 3 -1 0 -5 6 5 -1 4 73 3 4 -4 1 -5 3 4 -4 1 -3 |
| 16. | -1 3 5 4 17 -2 2 -3 1 4 3 1 -1 7 -14 0 1 2 -1 -8 1 -1 4 -3 -2 1 1 1 -2 1 1 -1 -2 1 10 3 1 -1 1 -1 2 0 -2 9 -1 1 -1 4 1 4 2 2 0 -1 1 1 1 -3 2 -7 |
| 17. | 1 0 2 3 20 -2 2 -3 1 4 -2 2 -3 1 1 -5 -3 1 -1 -7 1 -1 4 -3 -2 1 -1 4 -3 -2 -3 1 2 2 7 -3 1 4 -8 1 -3 1 4 -8 2 6 5 -1 4 25 -4 2 0 -5 3 -4 2 0 -5 3 |
| 18. | 1 -1 4 1 2 3 1 -1 7 -14 3 1 -1 7 -14 2 3 2 3 -9 1 -4 -3 8 -13 1 -4 -3 8 -12 -1 3 -5 4 -4 2 5 2 -1 -1 2 5 2 -1 -1 0 1 2 -1 -7 1 1 -3 2 -7 1 1 -3 2 -7 |
| 19. | 2 -5 3 -1 25 -3 2 1 4 -1 -3 2 1 4 -1 3 -7 3 -1 37 3 3 -4 9 -3 1 3 1 5 8 1 -9 6 7 62 2 0 -3 2 -5 5 4 -1 8 10 4 -6 3 1 35 4 1 -2 3 3 4 1 -2 3 3 |
| 20. | 1 3 2 3 -3 -3 2 -1 5 -17 -3 2 -1 5 -17 2 8 2 8 -6 2 -1 1 4 -11 2 -1 1 4 -11 -1 0 -4 -1 2 1 2 0 10 -26 -5 1 -2 1 -8 -2 -4 -3 -6 3 2 1 0 1 2 -6 2 -2 10 –30 |
| 21. | 2 -1 3 -4 -9 -3 2 1 4 -1 1 -1 0 8 10 1 0 -1 0 0 1 3 1 5 8 1 -5 1 2 17 2 1 1 -1 -4 5 4 -1 8 11 -1 3 -1 2 -9 0 1 -1 5 6 4 1 -2 3 3 1 1 0 4 4 |
| 22. | 1 3 2 3 11 -3 2 -1 5 -17 -3 -4 -3 -3 -32 2 8 2 8 32 2 -1 1 4 -11 -4 2 -1 2 5 -1 0 -4 -1 1 -5 1 -2 1 -8 1 -4 2 -2 -9 -2 -4 -3 -6 -19 -6 2 -2 10 -36 -6 -6 -2 -3 –34 |
| 23. | 2 -1 3 -4 -23 3 -7 1 -1 22 -3 0 -4 -2 7 1 0 -1 0 -1 3 -3 0 5 17 2 3 0 -1 4 2 1 1 -1 -4 -1 3 -1 2 -9 -3 1 -4 1 2 0 1 -1 5 20 1 1 0 4 4 -2 -4 0 -2 –14 |
| 24. | 2 -1 3 -4 -11 1 -1 0 8 12 5 3 -2 1 5 0 0 2 1 2 1 -5 1 2 17 1 2 2 2 4 2 1 1 -1 15 -1 3 -1 2 -9 1 2 -2 -1 -5 0 1 -1 5 27 1 1 0 4 4 3 -1 -2 0 8 |
| 25. | 2 -5 3 -1 -19 -3 -2 -3 2 -8 1 0 2 0 -1 3 -1 3 -1 -18 0 -3 -4 -3 -30 0 -3 2 -2 2 1 -2 0 6 25 -3 -1 2 0 1 -1 -3 0 -2 -13 0 1 1 -3 -15 21 6 -8 -7 -19 3 1 -1 0 20 |
| 26. | 1 2 1 -1 -1 3 0 1 -2 -1 -1 -3 -1 -3 7 2 -1 1 0 11 1 1 -4 -2 1 -4 1 1 -1 -3 1 -1 2 4 28 1 0 2 2 6 -4 1 2 -1 9 2 1 -1 3 31 5 1 -1 -2 6 1 3 0 3 -9 |
| 27. | 2 -5 3 -1 -8 -2 1 -4 -4 -7 2 -1 3 0 -7 1 -1 1 2 11 2 -3 -4 -3 -22 -4 3 -5 -2 10 1 -2 0 6 42 3 -1 -3 3 -9 2 -2 2 2 -4 0 1 1 -3 -24 3 -3 -11 -4 -38 -1 3 3 3 26 |
| 28. | 2 -5 3 -1 26 -4 -3 -3 2 4 0 1 -1 8 6 1 -1 1 2 10 2 2 -1 2 6 -4 -1 2 1 -8 1 -2 0 6 19 -4 3 -2 3 -5 -2 2 0 -4 –14 0 1 1 -3 -8 -6 2 -6 7 5 -2 -4 3 -3 –20 |
| 29. | 1 3 4 -1 -29 0 -3 3 -3 0 0 0 2 -2 -9 -1 1 0 1 1 -1 -2 -3 1 0 -1 2 2 1 12 4 -2 2 -6 -22 2 -2 2 -4 2 1 -2 0 -3 -10 2 4 1 -1 -37 3 -3 8 -8 2 -4 0 0 3 7 |
| 30. | 9 7 -5 2 34 -4 0 3 2 12 2 0 2 -1 1 1 -1 3 -1 2 -4 2 3 1 17 -1 -4 -3 1 9 4 3 -1 0 14 -1 3 1 -1 11 -1 1 1 -4 -16 2 -1 4 1 5 3 1 -2 -2 -6 0 -3 0 -4 6 |
| Номер ресурса | Объем ресурса | Номер продукции | |
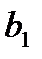
| 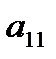
| 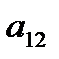
| |
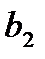
| 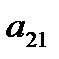
| 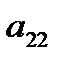
| |
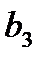
| 
| 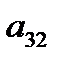
| |
| Ограничения по выпуску | 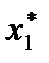
| 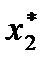
| |
| Прибыль | 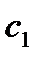
| 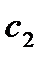
|
Задание 4. Для изготовления двух видов продукции имеются три вида ресурсов, объемы которых ограничены величинами 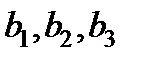 соответственно. Расход
соответственно. Расход 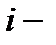 го вида ресурса на изготовление одной единицы
го вида ресурса на изготовление одной единицы  го вида продукции равен
го вида продукции равен 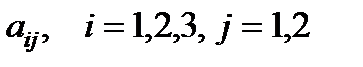 . Объем выпуска каждого из видов продукции ограничен числом
. Объем выпуска каждого из видов продукции ограничен числом 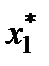 и
и 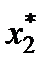 единиц, а прибыль, получаемая от реализации одной единицы изготовленной продукции равна
единиц, а прибыль, получаемая от реализации одной единицы изготовленной продукции равна 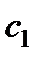 и
и 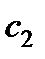 соответственно. Данные задачи могут быть представлены в матрично-векторном виде
соответственно. Данные задачи могут быть представлены в матрично-векторном виде 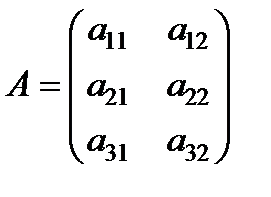 ,
, 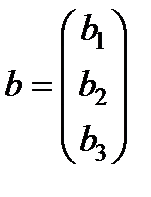 ,
, 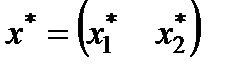 ,
, 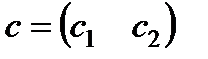 , или в форме таблицы.
, или в форме таблицы.
Требуется сверстать план выпуска продукции (число единиц продукции по каждому виду), удовлетворяющий принятым ограничениям и приносящий максимум прибыли после реализации выпущенной продукции.
| № Вар-та | № Вар-та | № Вар-та | |||
| 1. | 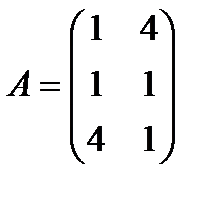 , , 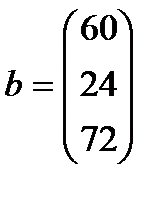 , , 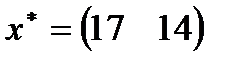 , , 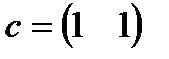
| 2. | 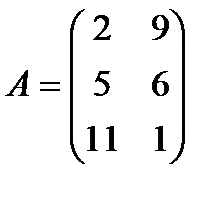 , ,  , , 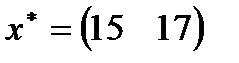 , , 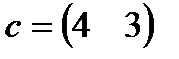
| 3. |  , , 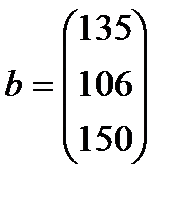 , , 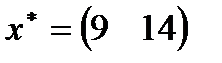 , , 
|
| 4. | 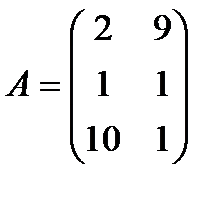 , ,  , , 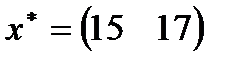 , , 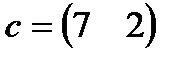
| 5. | 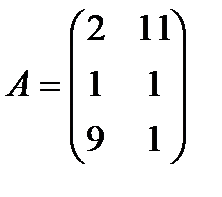 , , 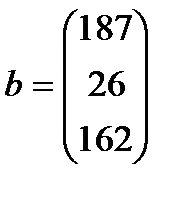 , , 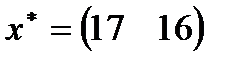 , , 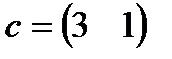
| 6. | 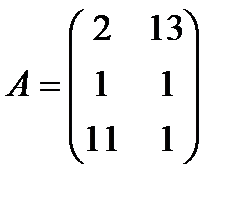 , , 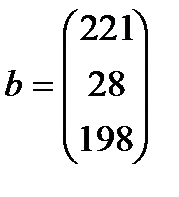 , , 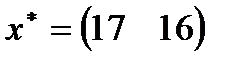 , , 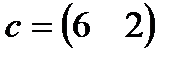
|
| 7. | 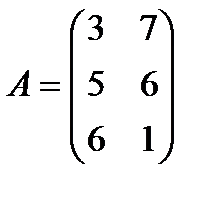 , , 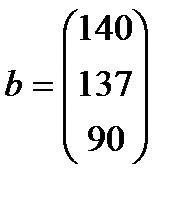 , , 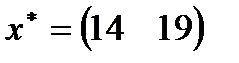 , , 
| 8. | 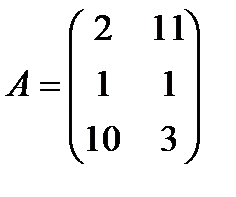 , , 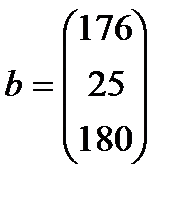 , , 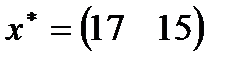 , , 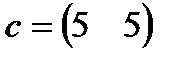
| 9. | 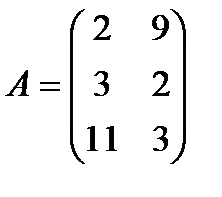 , , 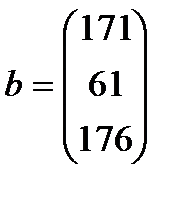 , , 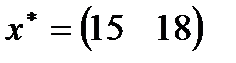 , , 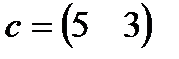
|
| 10. | 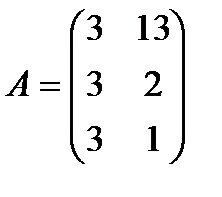 , , 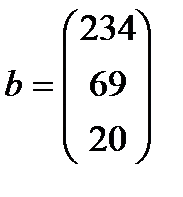 , , 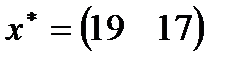 , , 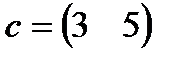
| 11. | 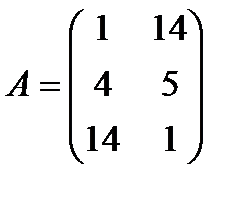 , , 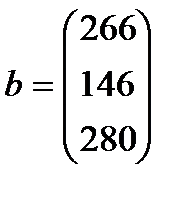 , , 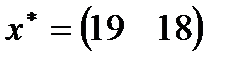 , , 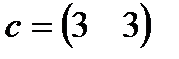
| 12. | 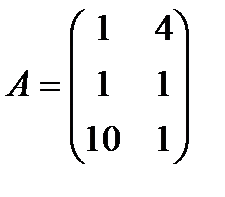 , , 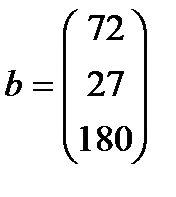 , , 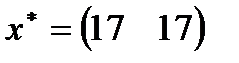 , , 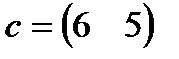
|
| 13. | 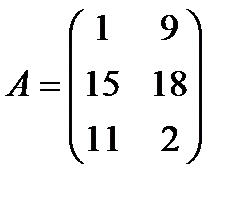 , , 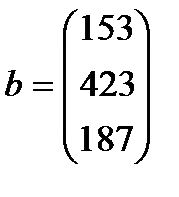 , , 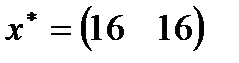 , , 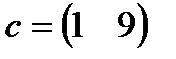
| 14. | 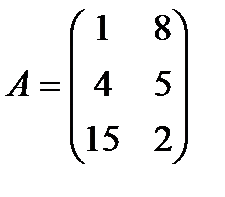 , , 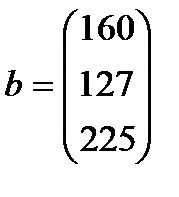 , , 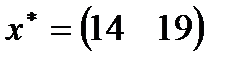 , , 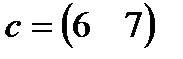
| 15. | 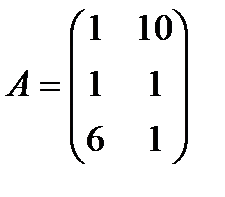 , , 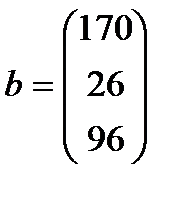 , , 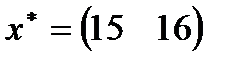 , , 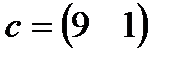
|
| 16. | 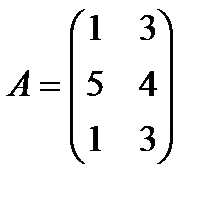 , ,  , , 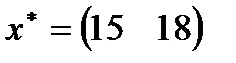 , , 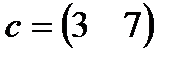
| 17. | 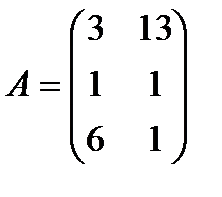 , , 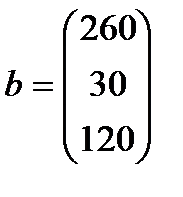 , ,  , , 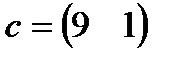
| 18. | 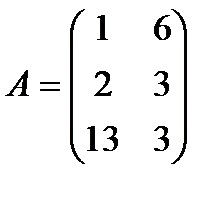 , ,  , , 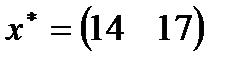 , , 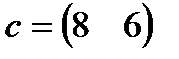
|
| 19. | 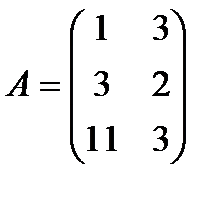 , , 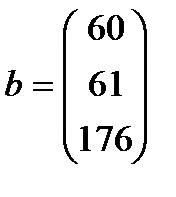 , , 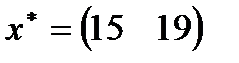 , , 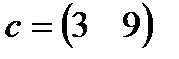
| 20. | 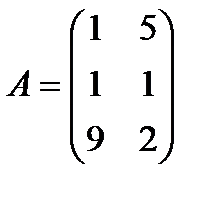 , , 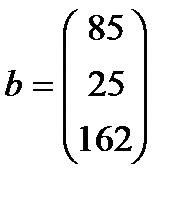 , , 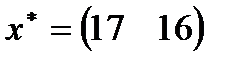 , , 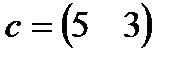
| 21. | 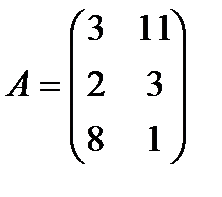 , , 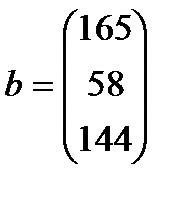 , , 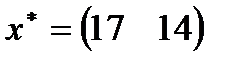 , , 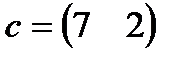
|
| 22. | 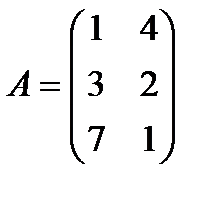 , , 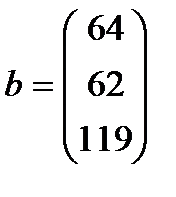 , , 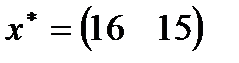 , , 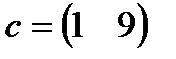
| 23. | 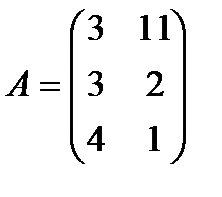 , , 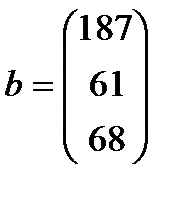 , , 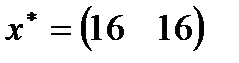 , , 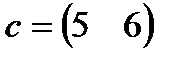
| 24. | 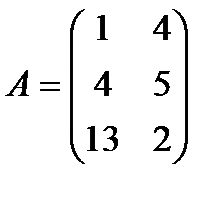 , , 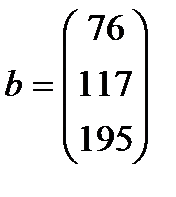 , , 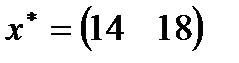 , , 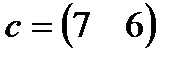
|
| 25. | 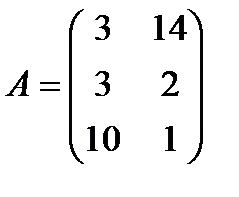 , , 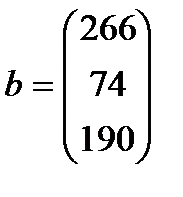 , ,  , , 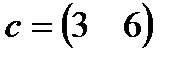
| 26. |  , , 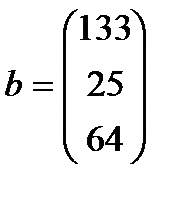 , , 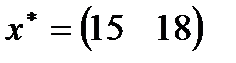 , , 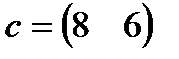
| 27. | 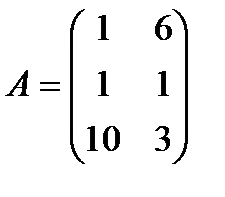 , , 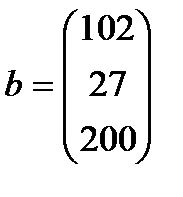 , , 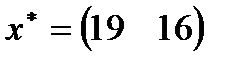 , , 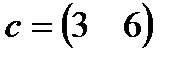
|
| 28. | 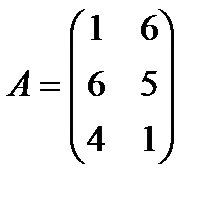 , , 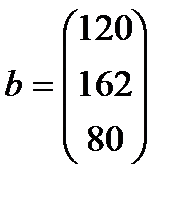 , , 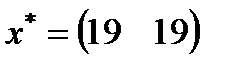 , , 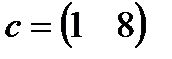
| 29. | 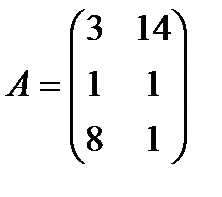 , , 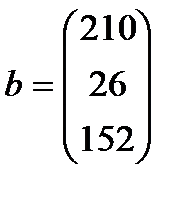 , , 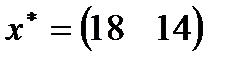 , , 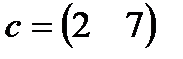
| 30. | 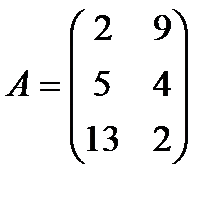 , , 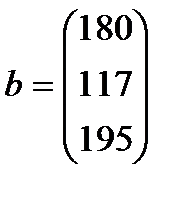 , , 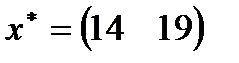 , , 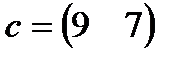
|
 2015-04-20
2015-04-20 490
490








