Расчет динамических характеристик шпиндельного узла

В ряде случаев динамическое качество станка определяется в основном динамическими характеристиками шпиндельного узла. Для расчета шпиндель­ных узлов с несколькими опорами или несколькими подшипниками в одной опоре (статически неопределимой) наиболее подходит метод начальных пара­метров в матричной формулировке, называемый методом переходных матриц или методом продолжения [35, 51, 58]. Целью расчета является определение амплитуд установившихся: колебаний шпинделя на его переднем конце при условии, что в процессе резания со стороны привода на шпиндель действуют гармонические возмущающие силы.

Шпиндель представляют как балку ступенчато-переменного сечения на линейно-упругих опорах с вязким демпфированием, пропорциональным ско­рости колебаний. Балку разбивают на участки. Их границами считают сече­ния, в которых изменяется момент инерции поперечного сечения шпинделя или расположена опора, находится сосредоточенная масса (патрон, шкив, зуб­чатое колесо), действует внешняя сосредоточенная нагрузка (сила, изгибаю­щий момент), имеет место скачкообразное изменение распределенной нагруз­ки.

На рис. 6.18 представлена схема шпиндельного узла с разбиением шпин­деля на три участка длиной 1₁,1₂ и I₃,ограниченные сечениями0,1,2 и3.На заднем и переднем концах расположены сосредоточенные массы: шкив ремен­ной передачи 4 (или зубчатое колесо) и патрон 5. В процессе резания на шпин­дель действуют возмущающая гармоническая сила F₀ (t) и гармоническая сила F₃ (t) со стороны привода, являющиеся функциями времени t.

Для q- го сечения вводим следующие обозначения: 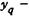амплитуда перемещений; 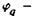угол поворота сечения; 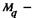изгибающий момент; 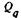— поперечная сила для q-гo участка; т — распределенная масса (масса единицы длины); 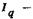момент инерции сечения; Е - модуль упругости материала; 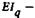изгибная жесткость. Буквами j и h обозначаем радиальную жесткость и коэффициент демпфирования опор.

Дифференциальное уравнение свободных колебаний ^-го участка шпин­деля:

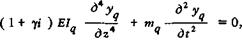
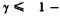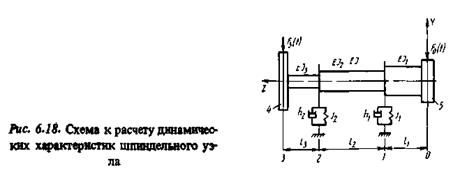
где коэффициент демпфирования, учитывающий рассеяние энергии колебаний в материале шпинделя; 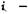мнимая единица; 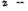координата вдоль оси шпинделя.

Если решение искать в виде

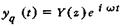
где 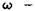круговая частота колебаний; У(z) — функция формы колебаний, то уравнение формы колебаний приобретает вид

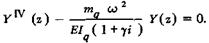(6.4)

В общем случае приложения внешней нагрузки рассматриваемый шпин­дельный узел описывается следующим дифференциальным уравнением:

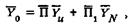(6.5)

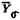где и 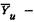векторы параметров на свободных концах шпинделя (в сечениях с номерами Q_ и и);

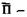матрица (4x4), равная произведению всех

матриц перехода;

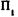— матрица (4x4), равная произведению матриц перехо­да, соответствующих участкам шпинделя, расположенным левее сечения N, где приложена внешняя нагрузка;

Y_N — вектор параметров в сечении N.

Векторы параметров на свободных концах рассматриваемого шпинделя длиной l без учета свободной нагрузки

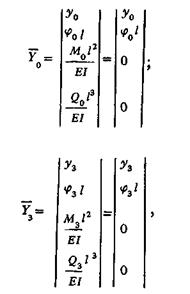
где через EI обозначена изгибная жесткость участка наибольшей длины, т.е. межопорной части шпинделя: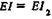

С учетом граничных условий из уравнения (6.5) находим прогиб у и угол наклона y ₀ в начальном сечении. С использованием переходных матриц сечений и участков шпинделя методом обратной прогонки определим прогиб и угол поворота в любом сечении.

Переходные матрицы рассмотрим более подробно. Патрон, находящийся на переднем конце шпинделя, т.е. в нулевом сечении, представим в виде груза, имеющего сосредоточенную массу 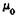и момент инерции 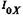относительно оси X. Амплитудные значения его колебаний равны 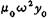и 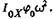При переходе через нулевое сечение параметры матрицы 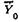преобразуются с по­мощью матрицы сосредоточенной массы

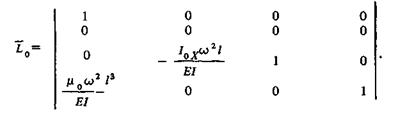
Параметры на концах первого участка связаны матрицей перехода через участок

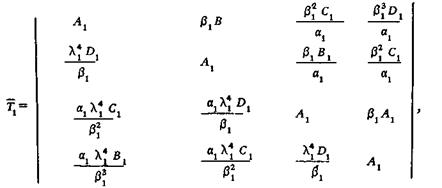
получаемой в результате решения дифференциального уравнения (6.4). Здесь А_х, В_х, С_г, D_x — функции, которые могут быть представлены в виде степен­ных рядов;

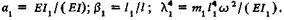
Скачок поперечной силы при переходе через опору 1, равный ее реакции с учетом упругой и диссипативной составляющих, описывается матрицей опоры

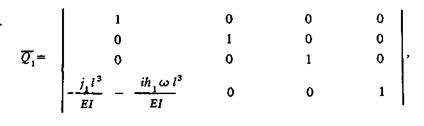
Аналогично записываются остальные переходные матрицы: 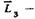сосредоточенной массы в третьем сечени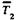и; и 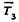— второго и третьего участков; 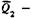второй опоры. Переход от правого (нулевого) сечения шпинделя к лево­му описывается переходной матрицей, равной произведению всех переходных матриц:

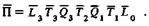
В результате перехода получаем матричное уравнение

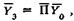(6.6)

пригодное при отсутствии внешней нагрузки на шпиндель. Из этого уравнения определяют собственные частоты колебаний шпинделя. При этом сначала на­ходят детерминант уравнения, являющийся функцией круговой частоты со, а затем ряд собственных частот, при которых детерминант обращается в ноль. С учетом внешней нагрузки в первом и третьем сечениях уравнение (6.6) для рассматриваемого шпинделя приобретает вид

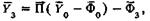(6.7)

где

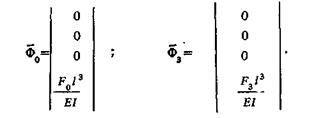
Из уравнения (6.7) определяют частотные передаточные функции системы 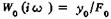по воздействию со стороны процесса резания (при F₃ = 0), системы 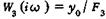по воздействию со стороны привода (при F = 0), а также амплитудно-фазовую частотную характеристику системы шпиндельного узла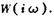

По результатам анализа динамических характеристик производят оптими­зацию параметров шпиндельного узла. Для этого разработан комплекс про­грамм расчета этих характеристик на ЭВМ в пакетном и диалоговом режимах.