Разложение функций в степенные ряды
Пусть функция 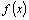 бесконечно дифференцируема в
бесконечно дифференцируема в 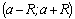 и является суммой степенного ряда:
и является суммой степенного ряда:
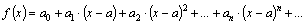
| (1) |
где 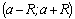 –интервал сходимости ряда (1). В этом случае говорят, что функция
–интервал сходимости ряда (1). В этом случае говорят, что функция 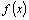 разлагается в степенной ряд в окрестности точки
разлагается в степенной ряд в окрестности точки 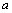 или по степеням
или по степеням 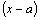 . Определим коэффициенты
. Определим коэффициенты 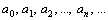 этого ряда, для чего продифференцируем
этого ряда, для чего продифференцируем 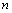 раз ряд (1).
раз ряд (1).
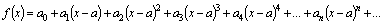
| (1) |
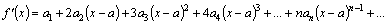
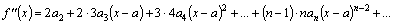
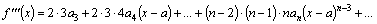
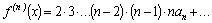
Все ряды имеют интервалы сходимости 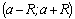 . При
. При 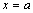 из полученных тождеств получаем:
из полученных тождеств получаем: 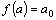 ,
, 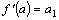 ,
, 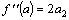 ,
, 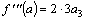 , …,
, …, 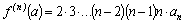 , … Отсюда находим коэффициенты степенного ряда (1):
, … Отсюда находим коэффициенты степенного ряда (1): 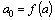 ,
,  ,
, 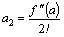 ,
, 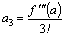 , …,
, …, 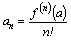 , … Подставляем полученные значения коэффициентов в ряд (1), получаем
, … Подставляем полученные значения коэффициентов в ряд (1), получаем
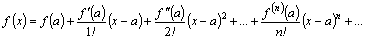
| (2) |
Ряд (2) называется рядом Тейлора для функции 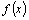 в точке
в точке 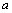 . В частном случае при
. В частном случае при 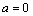 ряд (2) принимает вид:
ряд (2) принимает вид:
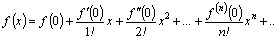
| (3) |
и называется рядом Маклорена.
Таким образом, если функция 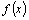 является суммой степенного ряда, то этот ряд называется рядом Тейлора для функции
является суммой степенного ряда, то этот ряд называется рядом Тейлора для функции 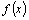 .
.
Пусть теперь дана бесконечно дифференцируемая в точке 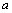 функция
функция 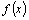 . Составим для нее формально ряд Тейлора:
. Составим для нее формально ряд Тейлора: 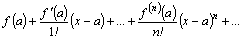 .
.
 2015-04-20
2015-04-20 259
259






