| ФИО | Личностная тревожность | |
| до тренинга | после тренинга | |
| 1.И.В. Л. | ||
| 2.Я. Е. А. | ||
| 3.К С. И | ||
| 4.Р М.Н. | ||
| 5.Н.М.Т. | ||
| 6.Е. Л.П. | ||
| 7.Л. К. С. | ||
| 8.Т. А. П. | ||
| 9.Б. В. В | ||
| 10.С М.А | ||
| 11.В. П. Р. | ||
| 12.Ч. Н. Г. | ||
| 13.А.С.П. | ||
| 14.В.С.К. | ||
| 15.В.П.П. | ||
| 16.Л.Г.Т. | ||
| 17.Т.И.Ч. | ||
| М (среднее) | 4,65 | |
| D (дисперсия) | 1,12 | 2,12 |
| SD(стандартное отклонение) | 1,06 | 1,46 |
| А (ассиметрия) | 0,10 | -0,82 |
| Е (эксцесс) | -1,27 | 0,42 |
Для первой выборки (до начала тренинга «Уверенное поведение») проведем расчеты для его участников, применив методику Плохинского Н.А.
Сформулируем гипотезы:
Нулевая гипотеза (Н0) — распределение эмпирической случайной величины данных, измеренных до проведения тренинга, отличается от нормального закона распределения.
Альтернативная гипотеза (Н1) — распределение эмпирической случайной величины подчиняется нормальному закону распределения.
Применим критерии Плохинского.
А=0,10; ΔА= 0,548; qА =0,10/0,548 = 0,183 <3
E=-1,27; ΔЕ = 2*0,548 =1,095; qE= 1,27 / 1,095 = 1,159 <3, где ошибки А и Е
По критерию Плохинского эмпирическое распределение достоверно можно считать распределенным нормально.
Акр= 1,549 Екр=3,876
А< Акр (0.1 <1.549); Е< Екр (1,27 <3,876)
Для второй выборки (после тренинга «Уверенное поведение») применим двойной составной критерий.
Сформулируем гипотезы:
Нулевая гипотеза (Н0) — распределение эмпирической случайной величины данных, измеренных после проведения тренинга, отличается от нормального закона распределения.
Альтернативная гипотеза (Н1) — распределение эмпирической случайной величины подчиняется нормальному закону распределения
Проверим выполнение первого условия Двойного критерия.
Проведем сравнение. Для этого необходимо рассчитать dэмп.
Сначала найдем среднее значение x=4.
Дополним таблицу 9 несколькими столбцами (Таблица 10):
Таблица 10
| ФИО | Личностная тревожность после тренинга | |x - 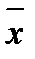 | |
| (|x - 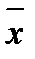 |)2 |)2
| |
| 1.И.В. Л. | ||||
| 2.Я. Е. А. | ||||
| 3.К С. И | ||||
| 4.Р М.Н. | ||||
| 5.Н.М.Т. | ||||
| 6.Е. Л.П. | ||||
| 7.Л. К. С. | ||||
| 8.Т. А. П. | ||||
| 9.Б. В. В | ||||
| 10.С М.А | ||||
| 11.В. П. Р. | ||||
| 12.Ч. Н. Г. | ||||
| 13.А.С.П. | ||||
| 14.В.С.К. | ||||
| 15.В.П.П. | ||||
| 16.Л.Г.Т. | ||||
| 17.Т.И.Ч. | ||||
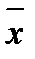 (среднее) (среднее)
| ||||
Сумма|x - 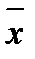 | |
| ||||
Сумма(|x - 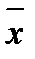 |)2 |)2
| ||||
| D (дисперсия) | 2,12 | |||
| SD(стандартное отклонение) | 1,46 |
ü Заполним третий столбец таблицы 10:.|x - 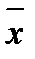 |
|
ü Просуммируем содержание столбца 1:
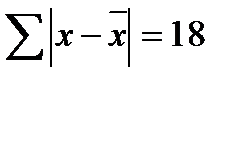
ü Затем найдем D и SD. Для этого возведем разность хпосле - 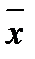 после в квадрат и запишем в столбец 4. Подсчитаем сумму:
после в квадрат и запишем в столбец 4. Подсчитаем сумму:
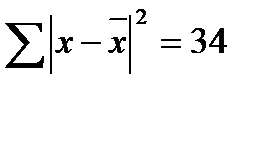
ü Поделим ее на (п — 1) = 17 — 1 = 16. Получим D = 2,12.
ü Возьмем квадратный корень из D:
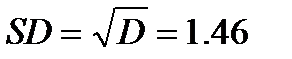
ü Пользуясь формулой dэмп. рассчитываем
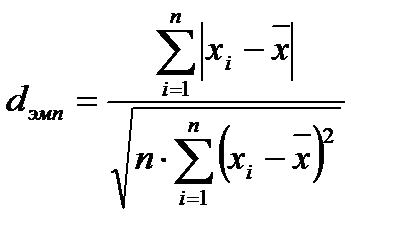
ü и получаем dэмп. = 0,75.
ü С помощью статистических таблиц определим d1 и d2 соответствующие объему выборки. d2 = 0,6829, d1 = 0,9137
ü.Т.к. dэмп>d2 и dэмп<d1 ( 0,75 > 0,6829 и 0,75 < 0,9137), то значит, dэмп удовлетворяет первому условию и можно переходить ко второму сравнению.
Проверим второе условие по двойному критерию.
Найдем z из статистических таблиц для объема выборки п = 17
z = 2,58.
Рассчитаем вспомогательное значение s, воспользовавшись рассчитанным стандартным отклонением SD,
s=SD ·z, s = 1,46*·2,58 =3,76
Если значение в столбце 3 |x - 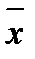 | будет больше рассчитанного s = 3,76, тов столбец 5 пишем 1, если нет, то 0. Затем считаем mэмп (сумму ячеек столбца 5): mэмп =0
| будет больше рассчитанного s = 3,76, тов столбец 5 пишем 1, если нет, то 0. Затем считаем mэмп (сумму ячеек столбца 5): mэмп =0
По статистической таблице находим mкр: mкр=1
Сравниваем mкр и mэмп: mкр>mэмп.
Значит, второе условие выполняется, следовательно, принимается гипотеза H1
Ответ: Принимается гипотеза Н1. Данные учащихся после исследования можно считать распределенными по нормальному закону.
Более подробно с двойным составным критерием можно познакомиться, используя дополнительную литературу [2].
 2015-04-20
2015-04-20 576
576








