Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков?
В данном случае пространство элементарных исходов состоит из трех равновозможных элементарных исходов: 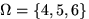 , и событию
, и событию 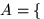 выпало четное число очков
выпало четное число очков 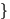 благоприятствуют 2 из них:
благоприятствуют 2 из них: 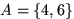 . Поэтому
. Поэтому 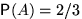 .
.
Посмотрим на этот вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек: 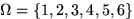 . Слова «известно, что выпало более трех очков» означают, что в эксперименте произошло событие
. Слова «известно, что выпало более трех очков» означают, что в эксперименте произошло событие 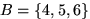 . Слова «какова при этом вероятность того, что выпало четное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении
. Слова «какова при этом вероятность того, что выпало четное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении 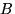 происходит и
происходит и 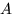 . Вероятность события
. Вероятность события 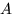 , вычисленную в предположении, что нечто о результате эксперимента уже известно (событие
, вычисленную в предположении, что нечто о результате эксперимента уже известно (событие 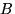 произошло), мы будем обозначать через
произошло), мы будем обозначать через 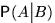 .
.
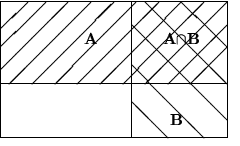
| Мы хотим вычислить отношение числа исходов, благоприятствующих 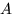 внутри внутри 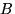 (то есть благоприятствующих одновременно (то есть благоприятствующих одновременно 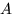 и и 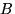 ), к числу исходов, благоприятствующих ), к числу исходов, благоприятствующих 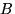 . . 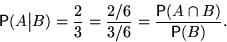
|
Какое отношение требуется вычислить, если элементарные исходы не являются равновозможными?
 2015-04-20
2015-04-20 408
408








