Выборочные характеристики и точечные оценки

Æ Выборочными характеристиками называются функции от наблюдений, приближённо оценивающие соответствующие числовые характеристики случайной величины.

Оценки параметров генеральной совокупности делятся на два класса: точечные и интервальные.

Точечныеоценки выражаются одним числом (точкой на числовой оси), находятся такие оценки по данным выборки и используются в дальнейшем вместо оцениваемого параметра. Точечная оценка, как функция от выборки, является случайной величиной и меняется от выборки к выборке при повторном эксперименте.

Интервальные оценки определяются двумя числами – концами интервала, который накрывает оцениваемый параметр.

В отличие от точечных оценок, которые не дают представления о том, как далеко от них может находиться оцениваемый параметр, интервальные оценки позволяют установить точность и надёжность оценок.

Если объём выборки 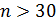, то при построении доверительного интервала для математического ожидания можно пользоваться нормальным законом распределения. В случае неизвестной дисперсии для определения ширины интервала используют несмещённую оценку дисперсии 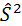и соответствующее выборочное среднее квадратическое отклонение [2] .

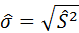К точечным оценкам предъявляют требования, которым они должны удовлетворять, чтобы хоть в каком-то смысле быть «доброкачественными». Это несмещённость, эффективность и состоятельность [1].

В качестве точечных оценок математического ожидания, дисперсии и среднего квадратического отклонения используют выборочные характеристики соответственно выборочное среднее, выборочная дисперсия и выборочное среднее квадратическое отклонение:

1) выборочное среднее: ;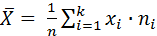

2) выборочная смещённая (неисправленная) дисперсия:

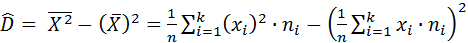, или

;

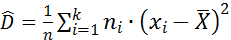3) выборочная несмещённая (исправленная) дисперсия:

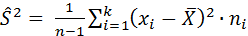, или ;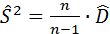

4) смещённое выборочное среднее квадратическое отклонение:

;

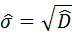5) несмещённое выборочное среднее квадратическое отклонение:

.

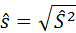Þ Примечание. Выборочное среднее 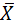есть несмещённая, эффективная и состоятельная точечная оценка математического ожидания, в то время как, выборочная дисперсия 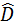является смещённой точечной оценкой дисперсии. В этом случае вводят исправленную (несмещённую) точечную оценку 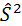дисперсии 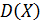[3].

В качестве других используемых на практике выборочных характеристик можно назвать выборочную моду 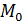и выборочную медиану 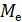[3].

Для наблюдений дискретной случайной величины:

- выборочная мода 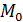равна значению варианты с наибольшей частотой ;

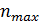- выборочная медиана 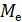равна значению варианты, стоящей в середине вариационного ряда, если число наблюдаемых вариант есть нечётное число;

- есличисло наблюдаемых вариант есть чётное число, тогда выборочная медиана 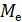равна полусумме двух соседних значений вариант, стоящих в середине вариационного ряда.

Медиана 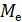есть серединный элемент.

В том случае, когда наблюдения проводятся для непрерывной случайной величины, то мода 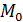и медиана 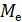определяются по следующим правилам.

Что касается моды 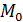, то сначала определяется модальный интервал, т. е. интервал с наибольшей частотой (или относительной частотой). Затем мода 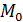вычисляется по формуле

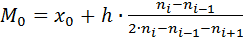, (1)

здесь 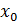- начало модального интервала, имеющего максимальную частоту 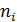, 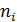- частота модального интервала, 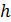- длина модального интервала, 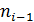и 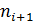- частоты интервалов соответственно предшествующего и последующего за модальным интервалом.

Медианой называют такое число 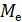, когда 50% вариант выборки меньше или равна этого значения, а 50% - больше или равна его, т. е. .

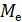Медиану определяем по следующему алгоритму:

1) найдите медианный интервал 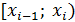. Это такой интервал, для которого накопленная частота 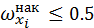, в этом случае медиана ;

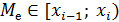2) вычислите медиану 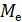по одной из формул:

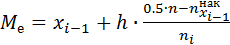, (2)

или

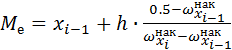, (3)

здесь 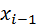- начало медианного интервала, 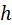- ширина медианного интервала, 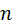- объём выборки, 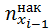- накопленная частота интервала, предшествующего медианному интервалу, 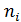- частота медианного интервала, 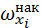- накопленная относительная частота медианного интервала, 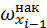- накопленная относительная частота интервала, предшествующего медианному интервалу.

?Упражнение 3. Найдите выборочное среднее, смещённую и несмещённую выборочные дисперсии, смещённое и несмещённое выборочные средние квадратические отклонения, моду 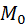и медиану 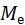по данному распределению выборки:

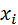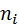Решение

В упражнении рассматривается дискретная случайная величина. Вычисления выполним в MS Excel.

Варианта	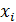Частота	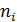Относительная частота	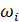Накопленная частота	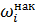Произведение варианты на частоту	Произведение квадрата варианты на частоту
		0,2	0,2
		0,3	0,5
		0,1	0,6
		0,4
Объём выборки:
Выборочное среднее:			4,2	20,4
Смещённая выборочная дисперсия:			2,76
Несмещённая выборочная дисперсия:			2,82
Смещённое выборочное среднее квадратическое отклонение:			1,66
Несмещённое выборочное среднее квадратическое отклонение:			1,68
Мода М0 = 3, наибольшая частота равна 15.
Медиана Ме = (3+5)/2 = 4 - среднее арифметическое двух серединных элементов.

Þ Примечание. В данном примере чётное количество вариант, а именно 4, это 2, 3, 5, и 6. Поэтому медиану определяем как среднее значение дух серединных элементов: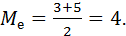

Несмещённая выборочная дисперсия вычисляется по формуле: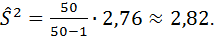

?Упражнение 4. Найдите выборочное среднее, выборочную дисперсию (смещённую и несмещённую), выборочное среднее квадратическое отклонение (смещённое и несмещённое) по данному распределению выборки:

Частичный интервал	[2,7)	[7,12)	[12,17)	[17,22)	[22,27)
Число наблюдений, попавших в интервал,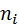

Решение

В данном упражнении наблюдения выполнены для непрерывной случайной величины. Здесь обязательно надо найти середины исследуемых интервалов. Именно таким образом поставленную задачу сведём к исследованию дискретной случайной величины. Вычисления выполним в MS Excel.

Частичный интервал	Частота	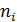Относитель- ная частота	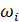Накоплен-ная относительная частота	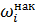Начало интервала	Конец интервала	Середина интервала	Произведе- ние середины интервала на частоту
[2; 7)		0,1	0,1			4,5	22,50
[7; 12)		0,2	0,3			9,5	95,00
[12; 17)		0,5	0,8			14,5	362,50
[17; 22)		0,12	0,92			19,5	117,00
[22; 27)		0,08				24,5	98,00
Объём выборки:							695,00
Длина интервала:					Выборочное среднее:	13,90
Мода М0:	14,21
Медиана Ме:	17,00

Þ Примечание. В данном примере максимальная частота 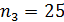, [12; 17) - модальный интервал, моду 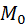вычисляем по формуле (1):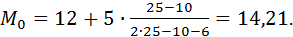

Интервал [7; 12) является медианным интервалом, поскольку накопленная относительная частота равна 0.3, а это значение меньше, чем 0.5, т. е. 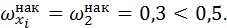Медиану можно вычислить по одной из формул (2) или (3):

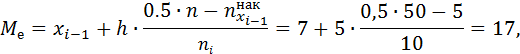
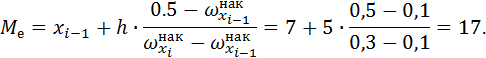
Найдём

- выборочную дисперсию (смещённую и несмещённую оценки);

- выборочное среднее квадратическое отклонение (смещённую и несмещённую оценки), для чего выполним дополнительные вычисления.