2015-04-20
824
Критическими точками функции называются точки, в которых производная функции равна нулю или не существует.
Достаточные условия существования экстремума (критерий нахождения точек экстремума): пусть функция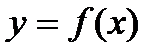 
непрерывна и дифференцируема в некоторой окрестности точки хо. Тогда:
1. если производная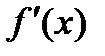 
при переходе через точку хо меняет знак с плюса на минус, то точка хо является точкой максимума;
2. если производная 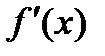при переходе через точку хо меняет знак с минуса на плюс, то точка хо является точкой минимума.
Из теорем вытекает следующий алгоритм:
1. Найдите область определения функции.
2. Найдите первую производную функции.
3. Определите критические точки (f'(xo) =0 или f'(xo) не существует) и выберите из них внутренние точки области определения.
4. На числовой оси отметьте критические точки и определите знаки производной слева и справа от каждой точки.
5. В соответствии с критериями найдите интервалы монотонности, выпишите точки экстремума функции (если они есть), вычислите значения функции в точках экстремума.
|
|
|
Пример 1. Найдите промежутки монотонности и экстремумы функции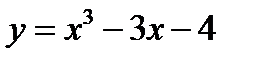 
.
Решение. 1. функция определена на множестве R.
2. Вычислим производную функции: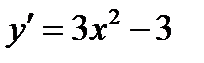 
.
3. Определим критические точки (у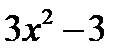' =0): 
=0;
х 1=-1 или х 2=1.
4. Отметим на числовой оси критические точки х 1=1 и х 2=5. Расставим знаки производной функции 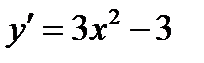на интервалах:
| т.min |
| т.max |
| -1 |
| х |
| + |
| + |
|
|
|
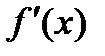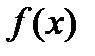5. По признаку возрастания и убывания, функция 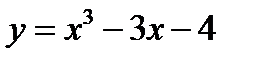возрастает при
х 
(-∞;-1] 
[1;+∞), убывает при х [-1;1].
По критерию нахождения точек экстремума х =-1 – точка максимума, х =1 – точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках:
= 
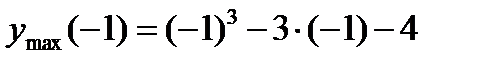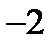- максимум функции;
= 
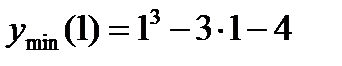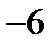- минимум функции.
Ответ: 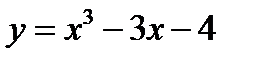возрастает при х (-∞;-1] [1;+∞), убывает при х [-1;1],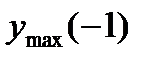 
= 
; 
= 
.
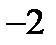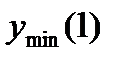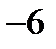Пример 2. Найдите промежутки монотонности и экстремумы функции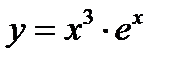 
.
Решение. 1. Функция определена на множестве R.
2. Найдем производную функции, используя правило производной произведения:
= 
= 
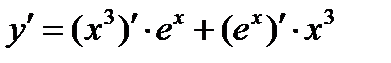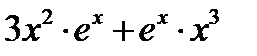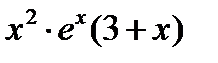
3. Определим критические точки: 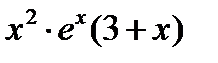=0;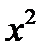 
=0 или 3+ х =0 
.
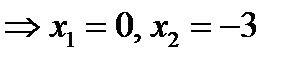4. На числовой оси отметим критические точки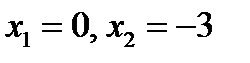 
. Исследуем знаки производной слева и справа от критических точек:
| + |
| т.min |
| -3 |
| х |
| + |
|
|
|
|
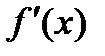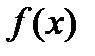5. Согласно критерию возрастания и убывания, функция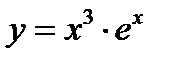 
возрастает при х 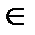[-3;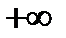 
], убывает при х 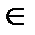(-∞;-3].
х =-3 – точка минимума,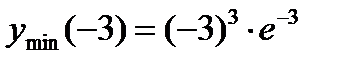 
= 
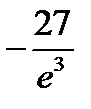- минимум функции.
Ответ: 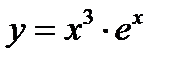возрастает при х 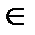[-3; 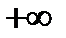], убывает при х 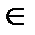(-∞;-3];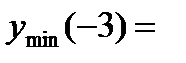 
.
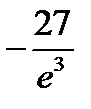Список литературы:
1. Богомолов Н.В. Сергиенко Л.Ю. Сборник дидактических заданий по математике: Учебное пособие для ссузов Изд. 3-е,стереотип. Дрофа 2010. -Глава 8, § 1, стр. 105, § 2, стр. 107.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 7, § 38-39, стр. 220-226.
|
|
|
3. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. – М.: Айрис-пресс, 2004. – 288 с. – Глава 5, §25, стр. 171-172.
