Цель: формирование умения находить неопределённые интегралы методом непосредственного интегрирования и методом подстановки
Задание для самостоятельной внеаудиторной работы:
& 6.1. Выучите определение первообразной функции, неопределенного интеграла и его свойства. Подготовьте таблицу неопределённых интегралов.
Выучите алгоритмы раскрытия неопределенностей вида 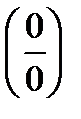 и
и 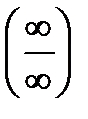 .
.
?6.2. Найдите интегралы методом непосредственного интегрирования:
а) 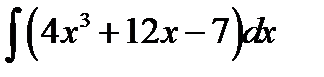 ; б)
; б) 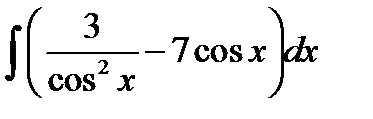 ; в)
; в) 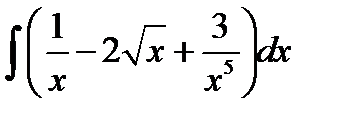 ;
;
г) 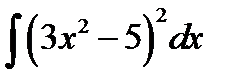 ; е)
; е) 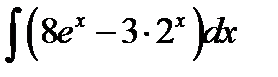 .
.
Методические указания по выполнению работы:
Напоминаем, что интегрировать, значит, находить первоначальной образ функции F(x) по известной производной f(x).
Функция F(x) называется первообразной для функции f(x) на интервале (а;b), если для всех x из этого промежутка верно: F'(x) = f(x).
Неопределённым интегралом от функции f(x) называется множество всех первообразных для функции f(x) и обозначается символом 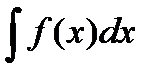 , т.е.
, т.е. 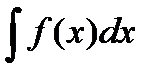 = F(x) + C.
= F(x) + C.
Свойства неопределенного интеграла:
1. 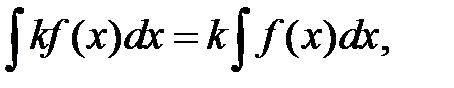 k- const, k
k- const, k 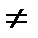 0;
0;
2. 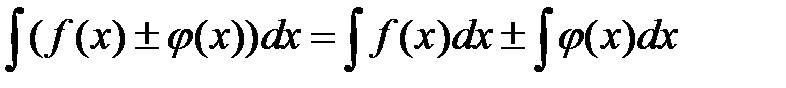 .
.
Первый метод – метод непосредственного интегрирования.
Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам.
Основные формулы интегрирования:
1. 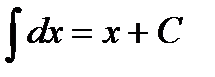 2. 2. 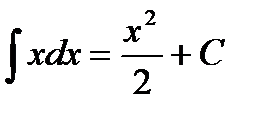 3. 3. 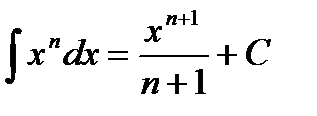 4. 4. 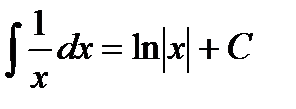 5. 5. 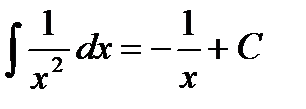 6. 6. 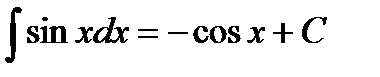 7. 7. 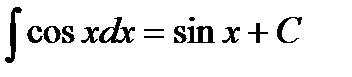 8. 8. 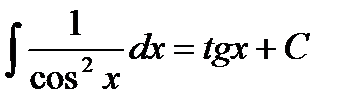 9. 9. 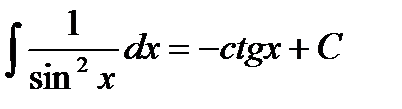 | 10. 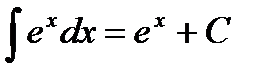 11. 11. 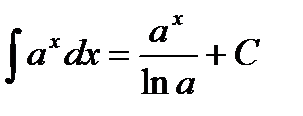 , а – const 12. , а – const 12. 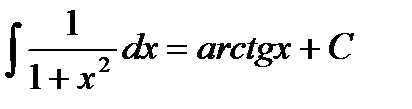 13. 13. 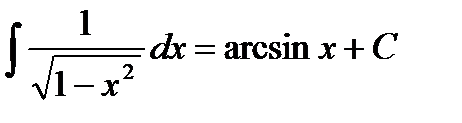 14. 14. 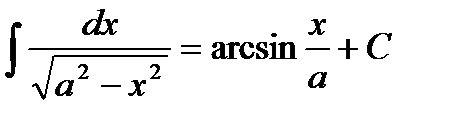 , а – const 15. , а – const 15. 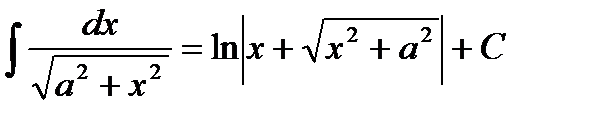 16. 16. 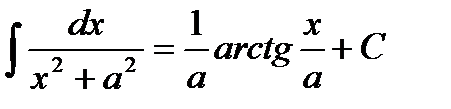 17. 17. 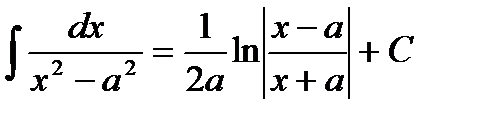 |
Пример 1. Найдите 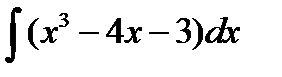 .
.
Решение.
Применим свойство 2: 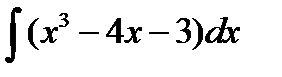 =
= 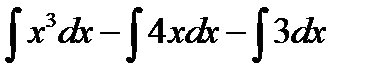 .
.
Применим свойство 1: 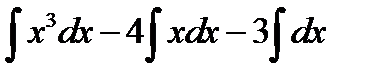 и воспользуемся табличными интегралами. Получим, что
и воспользуемся табличными интегралами. Получим, что 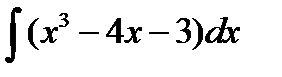 =
= 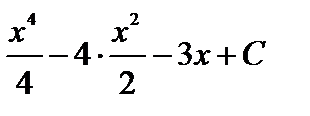 =
= 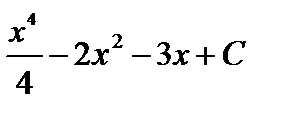 .
.
Ответ: 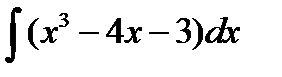 =
= 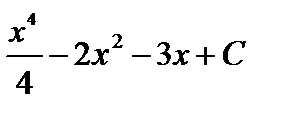 .
.
Пример 2. Найдите 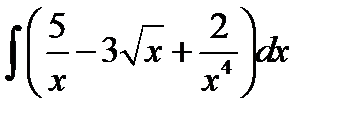 .
.
Решение. Применим свойства степени: а-п = 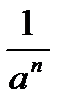 ;
; 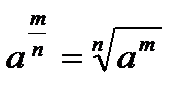 .
.
Тогда 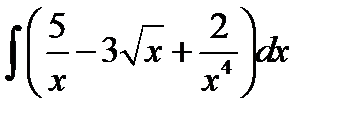 =
= 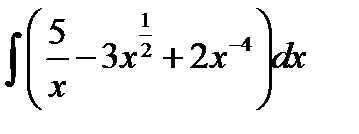 .
.
Применим свойства интеграла: 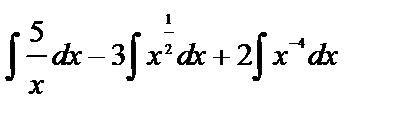 .
.
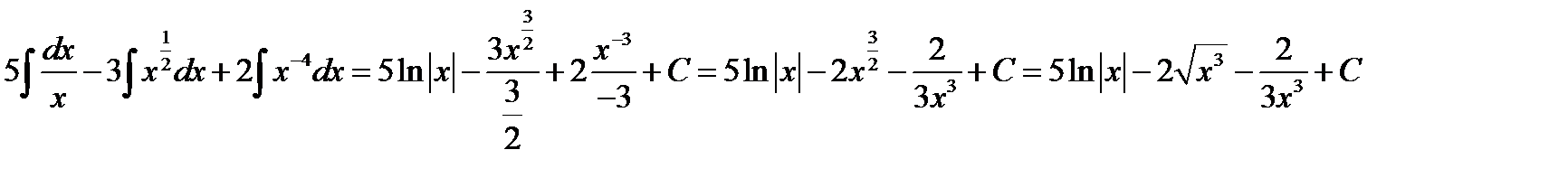
Ответ: 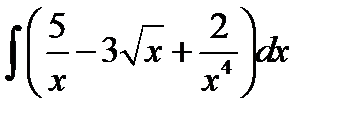 =
= 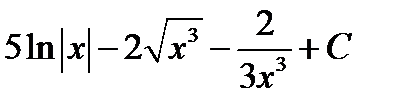 .
.
Пример 3. Найдите 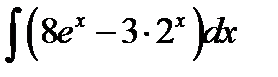 .
.
Решение. применяем свойства и табличные интегралы:
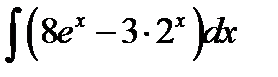 =
= 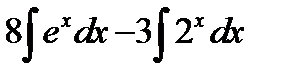 =
= 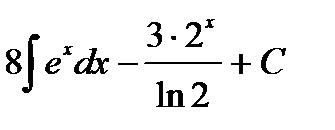 .
.
Ответ: 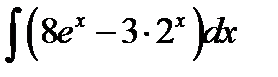 =
= 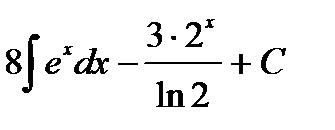 .
.
& 6.3. Разберите алгоритм нахождения неопределённого интеграла методом подстановки.
? 6.4. Найдите интегралы методом замены переменной (подстановки):
а) 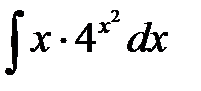 ; б)
; б) 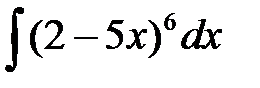 ; в)
; в) 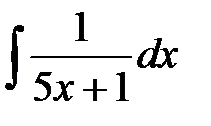 .
.
Методические указания по выполнению работы:
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 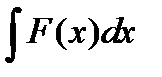 . Сделаем подстановку
. Сделаем подстановку 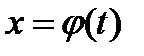 где
где 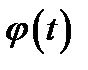 — функция, имеющая непрерывную производную.
— функция, имеющая непрерывную производную.
Тогда 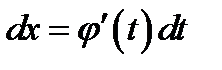 и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
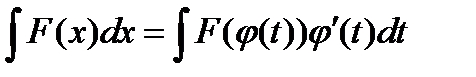
· Алгоритм вычисления неопределенного интеграла методом подстановки:
Рассмотрим нахождение интеграла от некоторых сложных функций на примерах.
Пример 1. Найдите 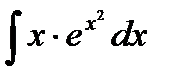 .
.
Решение. 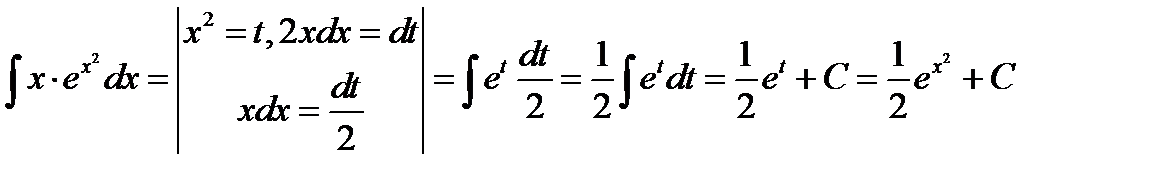
Ответ: 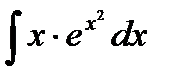 =
= 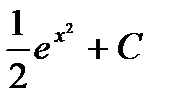
Пример 2. Найдите 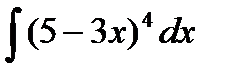 .
.
Решение. 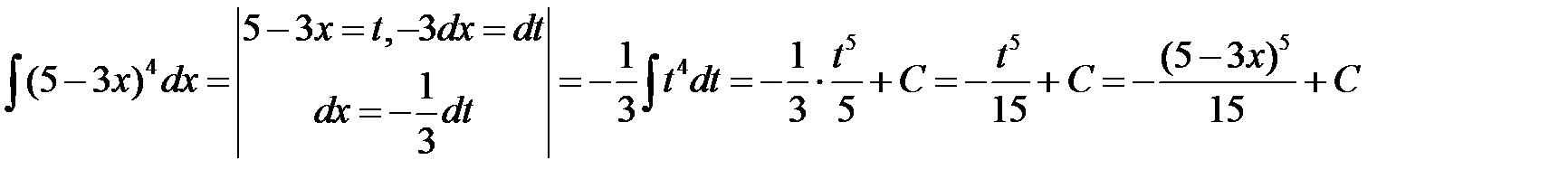
Список литературы:
1. Богомолов Н.В. Сергиенко Л.Ю. Сборник дидактических заданий по математике: Учебное пособие для ссузов Изд. 3-е,стереотип. Дрофа 2010 – Глава 6, § 1, стр. 76-80.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 6, § 31, стр. 188-198.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §2, стр. 182 – 192.
 2015-04-20
2015-04-20 3242
3242
