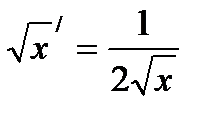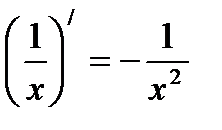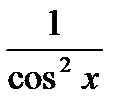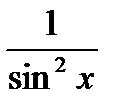Цель: формирование умения находить производные и дифференциалы функций, используя правила и формулы дифференцирования.
Задание для самостоятельной внеаудиторной работы:
& 2.1.Выучите определение производной функции в точке. Изучите таблицу «Формулы дифференцирования». Запомните правила дифференцирования функций.
& 2.2. Прочитайте о нахождении производной функции в точке.
? 2.3. Найдите производную функции в указанной точке:
а) 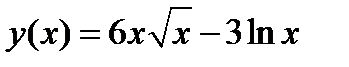 ,
, 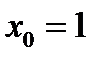 ;
;
б) 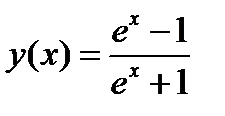 ,
, 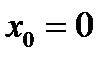 .
.
& 2.4. Выучите определение и формулу дифференциала функции.
? 2.5. Найдите дифференциал функции:
а) 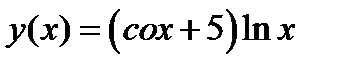 ;
;
б) 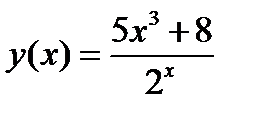 .
.
! 2.6. Найдите нули производной исходной функции: 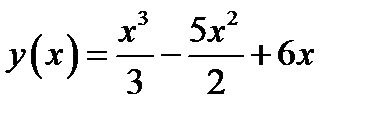 .
.
Методические указания по выполнению работы:
Необходимый теоретический материал:
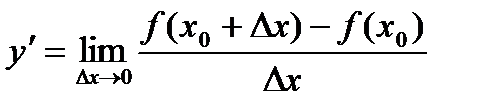 или или 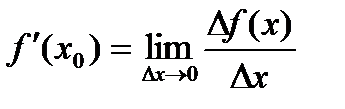 . . |
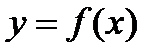 в точке
в точке 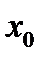 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Производная функции 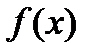 есть некоторая функция
есть некоторая функция 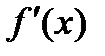 , производная из данной функции. Значение производной функции
, производная из данной функции. Значение производной функции 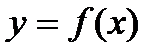 в точке
в точке 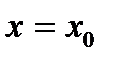 обозначается одним из символов:
обозначается одним из символов: 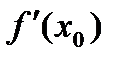 или
или 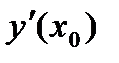 .
.
Функция 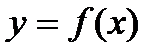 , имеющая производную в каждой точке интервала
, имеющая производную в каждой точке интервала 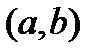 , называется дифференцируемой на этом интервале; операция нахождения производной функции называется дифференцированием.
, называется дифференцируемой на этом интервале; операция нахождения производной функции называется дифференцированием.
Для нахождения производных основных элементарных функций будем использовать следующую таблицу: «Формулы дифференцирования».
Формулы дифференцирования:
| 1. (ex)' = ex 2. (ax)' = ax lna 3. (ln x)' = 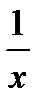 4. (logax)' = 4. (logax)' = 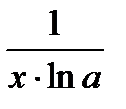
|
Нахождениепроизводной функции непосредственно по определению часто связано с определенными трудностями. Мы будем использовать ряд правил, называемых правилами дифференцирования.
Пусть u(х) и v(х) – дифференцируемые функции, с – константа. Тогда справедливы правила:
1. (cu)' = c u'
- (u ± v)' = u' ±v'
- (u∙v)' = u'v + v'u
-
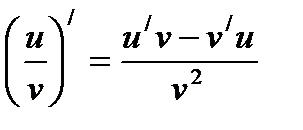
Пример 1. Найдите производную функции 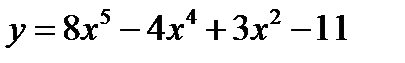 .
.
Решение: Для вычисления производной воспользуемся правилом (u ± v)' = u' ±v':
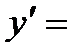
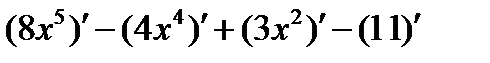 .
.
Постоянный множитель можно вынести за знак производной по правилу: (cu)' = c u'.
Следовательно, 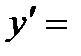
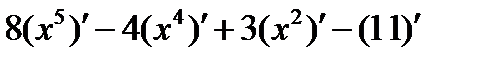 .
.
Обратимся к формулам производных:
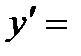
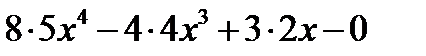 =
= 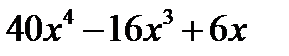 .
.
Ответ: 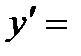
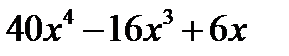 .
.
Пример 2. Найдите производную функции 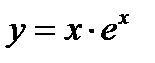 .
.
Решение. Воспользуемся правилом (u·v)' = u'v + v'u:
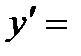
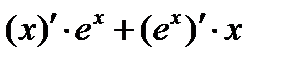 =
= 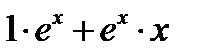 =
= 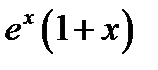 .
.
Ответ: 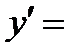
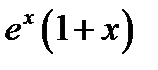 .
.
Пример 2. Найдите производную функции 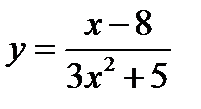 в точке
в точке 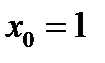
Решение. Воспользуемся правилом 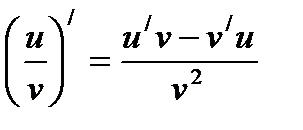 :
:
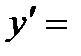
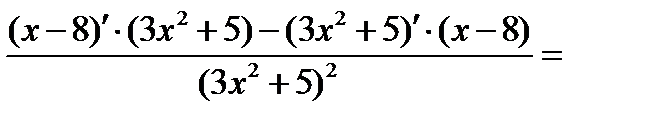
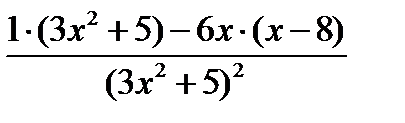 =
= 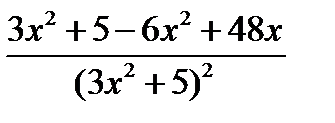 =
=
= 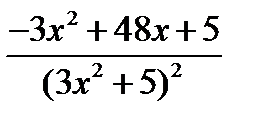 .
.
Для нахождения производной функции в точке в полученное выражение вместо аргумента подставим указанную точку.
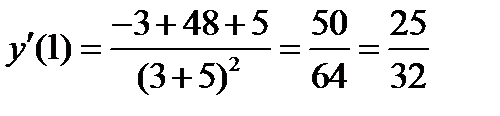
Ответ: 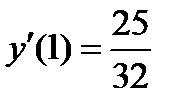 .
.
Дифференциалом функции 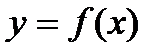 в точке
в точке 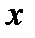 называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается 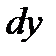 (или
(или 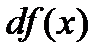 ):
): 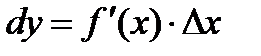 . Поскольку дифференциал независимой переменной равен приращению этой переменной:
. Поскольку дифференциал независимой переменной равен приращению этой переменной: 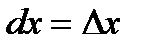 , дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной:
, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной: 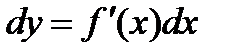
Пример 4. Найдите дифференциал функции 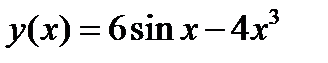 .
.
Решение. По формуле 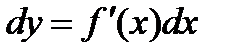 :
:
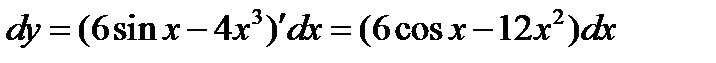 .
.
Ответ: 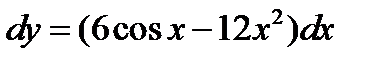 .
.
Список литературы:
1. Богомолов Н.В. Сергиенко Л.Ю. Сборник дидактических заданий по математике: Учебное пособие для ссузов Изд. 3-е,стереотип. Дрофа 2010.-Глава 7, §2, стр. 94-95; §3, стр. 95-98.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 7, § 33, стр. 205-210; § 36, стр.215-217; § 44, стр.240-245.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §4, стр. 208– 228; §6, стр. 245– 247.
 2015-04-20
2015-04-20 3533
3533