2015-04-20
1924
При решении уравнения F(x) = 0 прежде всего важно предварительно изучить расположение корней и заключить каждый корень в малую область, содержащую только один корень. Эту операцию удобно выполнять с использованием пакета MathCAD
(Лабораторная работа №2).
Для этой цели часто применяют графические методы. Если требуется найти только действительные корни уравнения, то для отыскания грубых значений корней можно построить график функции F(x) = 0 и найти абсциссы точек пересечения графика с осью X. Эти приближенные значения точек пересечения графика функции с осью X и принимают за начальные приближения к корням уравнения.
Если уравнение не имеет близких между собой корней, то этим способом они легко отделяются.
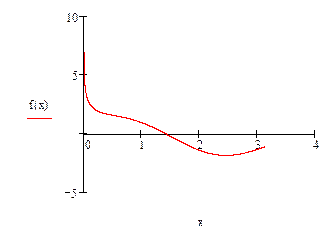Например
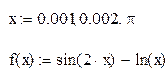
Иногда удобно представить уравнение F(x) = 0 в виде F1(x) = F2(x) и затем, построив графики функций y1 = F1(x) и y2 = F2(x), найти абсциссы точек пересечения, которые и будут приближенными значениями корней.
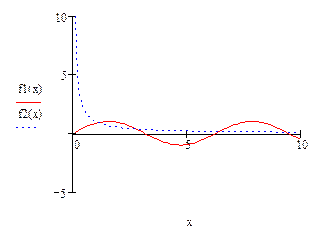Например
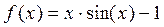
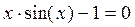
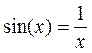
Корни уравнения симметричны относительно X=0. Поэтому мы можем рассматривать только положительные корни.
Значения x1, x2, x3 и еще нескольких корней можно довольно точно определить графически. Но на графике не будет xn для больших значений n. Значения xn при больших n будут близки к πn.
Эти значения можно уточнить.
Пусть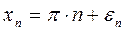 
,
где εn – некоторые небольшие добавки.
Тогда
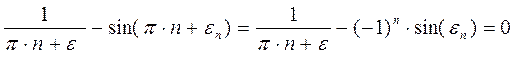
Т.к.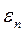 
очень мало, то можно принять 
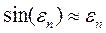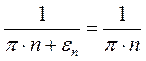
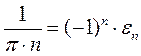и 
и 
.
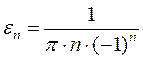В результате получим улучшенное значение корня 
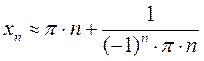
Преимущества графического метода решения – удобство и простота. Недостаток – данный метод применим только для грубого отделения корня.
