Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1), событие наступит ровно k раз (безразлично в какой последовательности) рассчитывается по формуле Бернулли:
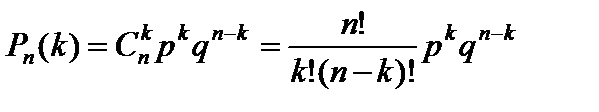 , (28)
, (28)
где q = 1 – p.
Вероятность того, что в n испытаниях событие A наступит: а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз; д) хотя бы один раз, находят соответственно по формулам
а) 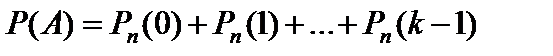 ; (29)
; (29)
б) 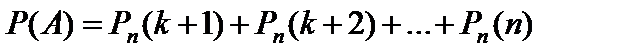 ; (30)
; (30)
в) 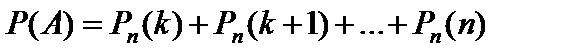 ; (31)
; (31)
г) 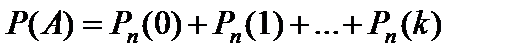 ; (32)
; (32)
д) 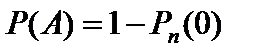 . (33)
. (33)
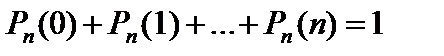 . (34)
. (34)
Пример 1.25. Монету бросают 5 раз. Какова вероятность того, что: а) герб выпал два раза; б) выпало более одного герба?
Решение. Пусть событие A – «выпадение герба при отдельном испытании», тогда
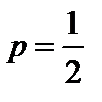 ;
; 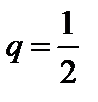 .
.
а) по формуле Бернулли:
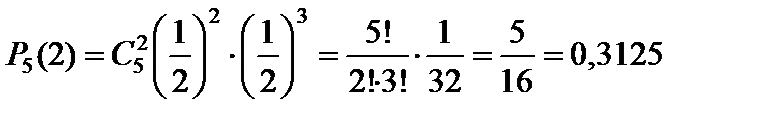 .
.
б) B – событие, что выпало более одного герба.
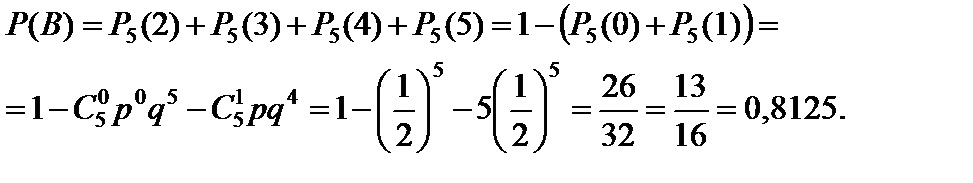
Пример 1.26. Фабрика выпускает 70 % продукции высшего сорта. Покупатель приобрел 5 изделий, изготовленных на данной фабрике. Какова вероятность того, что 2 из них – высшего сорта?
Решение. Обозначим через A – «приобретено изделие высшего сорта». Тогда p = 0,7, q = 1 – 0,7 = 0,3.
Вероятность того, что из пяти изделий 2 – высшего сорта, равна
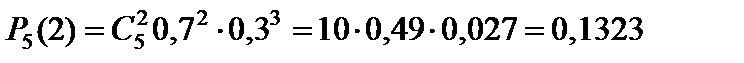 .
.
 2015-04-20
2015-04-20 2811
2811
