Два вектора плоскости линейно зависимы тогда и только тогда, когда они коллинеарны

Скрестите пальцы на столе, чтобы между ними был любой угол, кроме 0 или 180 градусов. Два вектора плоскости 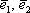линейно независимы в том и только том случае, если они не коллинеарны. Итак, базис 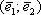получен. Не нужно смущаться, что базис получился «косым» с неперпендикулярными векторами различной длины. Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы

Любой вектор плоскости 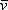единственным образом раскладывается по базису 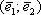: 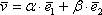, где 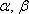– действительные числа. Числа 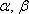называют координатами вектора в данном базисе.

Также говорят, что вектор 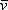представлен в виде линейной комбинации базисных векторов. То есть, выражение 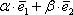называют разложением вектора 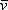по базису 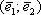или линейной комбинацией базисных векторов.

Например, можно сказать, что вектор 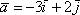разложен по ортонормированному базису плоскости 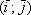, а можно сказать, что он представлен в виде линейной комбинации векторов .

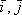Сформулируем определение базиса формально: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов 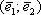, взятых в определённом порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов.

Существенным моментом определения является тот факт, что векторы взяты в определённом порядке. Базисы 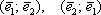– это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.

С базисом разобрались, но его недостаточно, чтобы задать координатную сетку и присвоить координаты каждому предмету вашего компьютерного стола. Почему недостаточно? Векторы являются свободными и блуждают по всей плоскости. Так как же присвоить координаты тем маленьким грязным точкам стола, которые остались после бурных выходных? Необходим отправной ориентир. И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:

Начну со «школьной» системы. Уже на вступительном уроке Векторы для чайников я выделял некоторые различия между прямоугольной системой координат и ортонормированным базисом 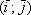. Вот стандартная картина:

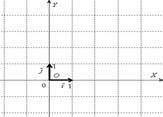
Когда говорят о прямоугольной системе координат, то чаще всего имеют в виду начало координат, координатные оси и размерность по осям. С другой стороны, создается впечатление, что прямоугольную систему координат вполне можно определить через ортонормированный базис 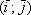. И это почти так. Формулировка звучит следующим образом:

Точка 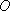плоскости, которая называется началом координат, и ортонормированный базис 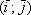задают декартову прямоугольную систему координат плоскости. То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами 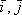. Именно поэтому, вы видите чертёж, который я привёл выше – в геометрических задачах часто (но далеко не всегда) рисуют и векторы, и координатные оси.

Думаю, всем понятно, что с помощью точки 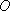(начала координат) и ортонормированного базиса 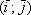ЛЮБОЙ ТОЧКЕ плоскости и ЛЮБОМУ ВЕКТОРУ плоскости можно присвоить координаты. Образно говоря, «на плоскости всё можно пронумеровать».Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку 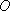и два ортогональных вектора 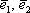произвольной ненулевой длины:

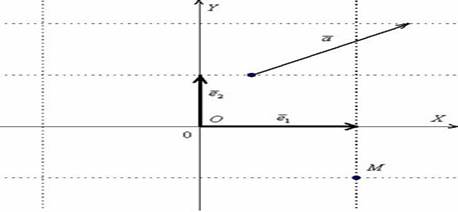
Такой базис называется ортогональным. Начало координат с векторами 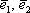задают координатную сетку, и любая точка плоскости, любой вектор имеют свои координаты в данном базисе. Например, 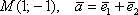или 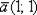. Очевидное неудобство состоит в том, что координатные векторы в общем случае имеют различные длины, отличные от единицы. Если длины равняются единице, то получается привычный ортонормированный базис.!! Примечание: в ортогональном базисе, а также ниже в аффинных базисах плоскости и пространства единицы по осям считаются УСЛОВНЫМИ. Например, в одной единице по оси абсцисс содержится 4 см, в одной единице по оси ординат 2 см. Данной информации достаточно, чтобы при необходимости перевести «нестандартные» координаты в «наши обычные сантиметры».

Как определить коллинеарность векторов плоскости?

Типовая вещь. Для того чтобы два вектора плоскости 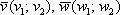были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны 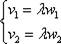. По существу, это покоординатная детализация очевидного соотношения .

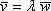Ранг нулевой матрицы = 0.

Ранг любого ненулевого вектора-строки (вектора-столбца) равен единице

И вообще – если в матрице произвольных размеров есть хотя бы один ненулевой элемент, то её ранг не меньше единицы.

Метод Гауса-приводим матрицу к ступенчатому виду.

В уравнении выражаем через х5 х4 х3… все остальные х