1. Найти значение коэффициента C и плотность распределения f (x) случайной величины X,функция распределения которой имеет вид:
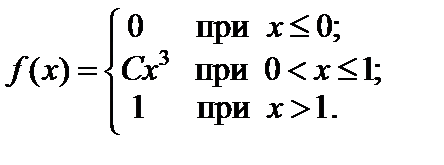
Ответ: C = 1; 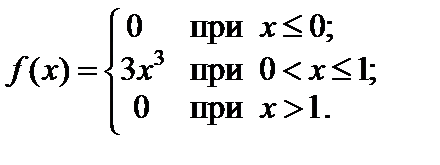
2. Найти вероятность того, что значение случайной величины X принадлежит интервалу (2; 3), если плотность распределения величины X задана функцией: 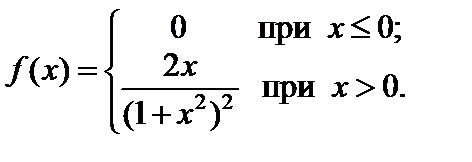
Ответ: 0,2.
3. Найти плотность распределения f (x) случайной величины Х, функция распределения которой имеет вид:
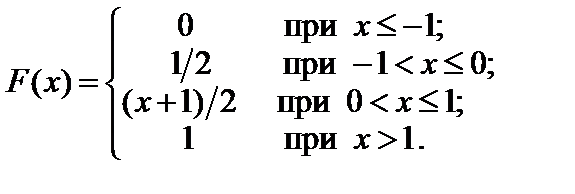
Какова вероятность того, что значение случайной величины X принадлежит интервалу (0,5; 1)?
Ответ: P = 0,5.
4. Найти интегральную функцию распределения F (x) и оценить вероятность попадания непрерывной случайной величины X в интервал (0,5; 1,5), если плотность распределения величины X имеет вид: 
Построить графики функций f (x) и F (x).
Ответ: 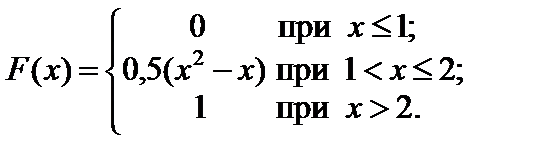 P (0,5 < Х < 1,5) = 0,375.
P (0,5 < Х < 1,5) = 0,375.
2.5. Числовые характеристики непрерывных
случайных величин
Математическое ожидание непрерывной случайной величины X определяется по следующей формуле:
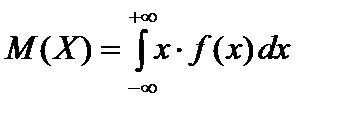 , (57)
, (57)
где 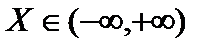 .
.
Дисперсия непрерывной случайной величины X:
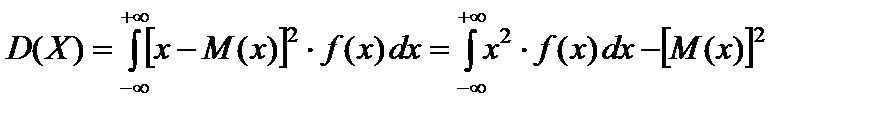 , (58)
, (58)
где 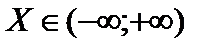 .
.
Все свойства M (X) и D (X), указанные выше в п. 2.3 для дискретных величин, сохраняются и для непрерывных величин.
Начальный момент порядка k непрерывной случайной величины X вычисляется по формуле
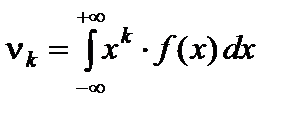 . (59)
. (59)
Центральный момент порядка k непрерывной случайной величины X, определяется равенством:
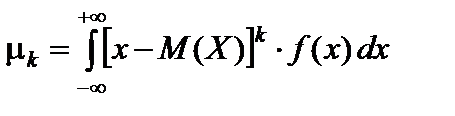 . (60)
. (60)
Если все возможные значения X принадлежат интервалу (a; b), то
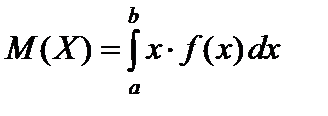 ; (61)
; (61)
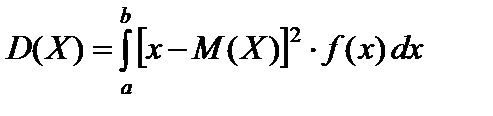 . (62)
. (62)
Пример 2.15. Найти математическое ожидание и дисперсию случайной величины X, которая задана дифференцированной функцией f (x) = 2 x в интервале (0; 1), вне его f (x) = 0.
Решение. 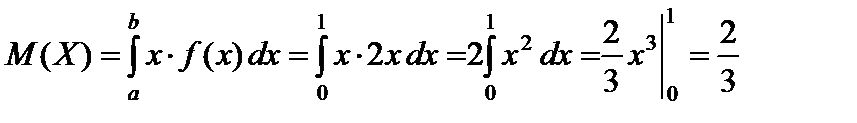 .
.
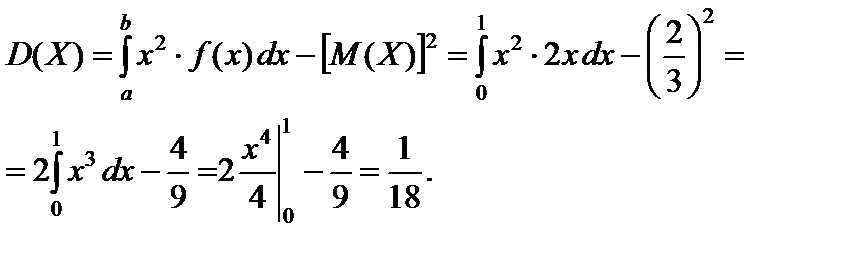
Пример 2.16. Найти математическое ожидание и начальный момент второго порядка случайной величины X, заданной интегральной функцией: 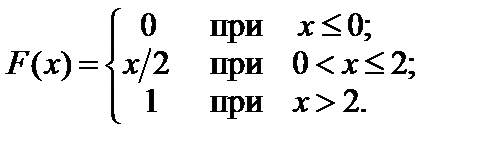
Решение. Найдем дифференциальную функцию X:

Используя формулу (61) рассчитаем математическое ожидание: 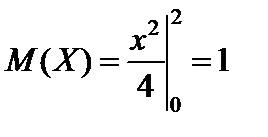 .
.
По формуле (60) найдем начальный момент второго порядка: 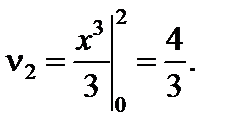
Пример 2.17. Случайная величина X задана интегральной функцией распределения: 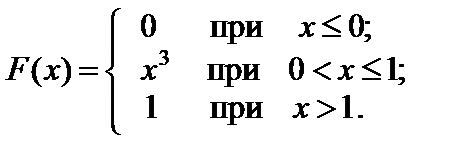
Необходимо выполнить следующее:
1. Найти плотность вероятности (дифференциальную функцию).
2. Вычислить математическое ожидание и дисперсию X.
3. Найти вероятность того, что X примет значение, принадлежащее интервалу (0,25; 0,5).
4. Построить графики функций F (x) и f (x).
Решение.
1. Найдем функцию плотности вероятности случайной величины X. Согласно формуле (51) плотность вероятности f (x) равна
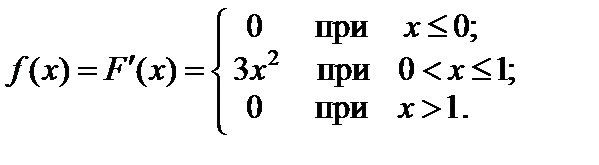
2. Вычислим математическое ожидание используя формулу (61):
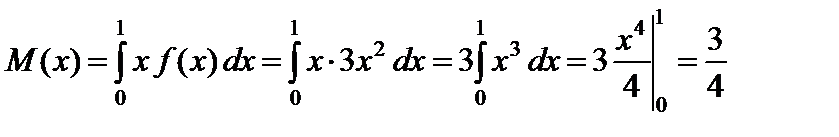 .
.
Дисперсию величины X рассчитаем по формуле (58):
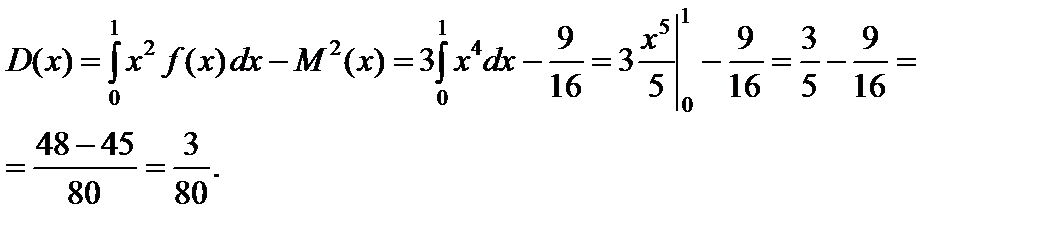
3. Согласно формуле (55) вероятность того, что случайная величина X примет значение, принадлежащее интервалу (0,25; 0,5) будет равна: 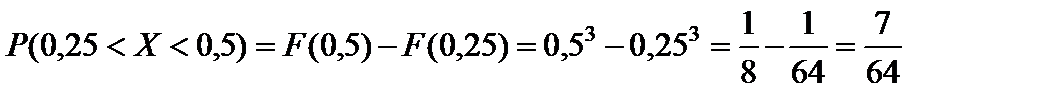 .
.
4. Построим графики функций F (x) и f (x). Графики функций F (x) и f (x) отражены на рис. 2.5 и 2.6.
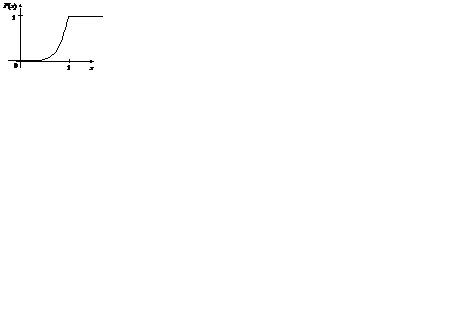 Рис. 2.5. График интегральной функции Рис. 2.5. График интегральной функции | 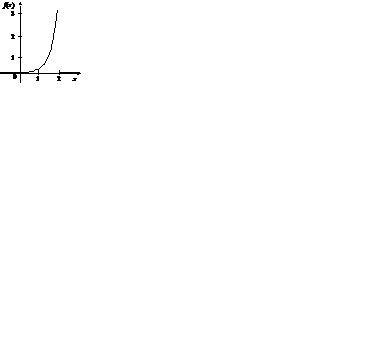 Рис. 2.6. График дифференциальной функции Рис. 2.6. График дифференциальной функции |
 2015-04-20
2015-04-20 3118
3118