2015-04-20
15167
Нормальным распределением, или распределением Гаусса, называется распределение с плотностью вероятностей
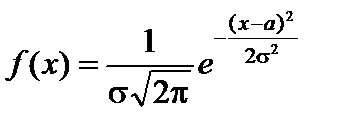, (65)
где a – математическое ожидание;
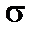– среднее квадратическое отклонение.
График функции P (x) называют нормальной кривой (рис. 2.9) a = 3, s = 1.
Рис. 2.9
Вероятность попадания значений нормальной случайной величины X в интервал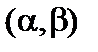 
определяется формулой
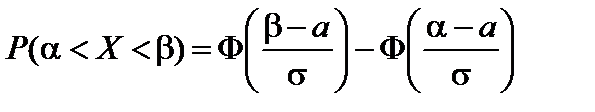, (66)
где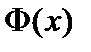 
– функция Лапласа.
Функция Лапласа описывается следующей формулой:
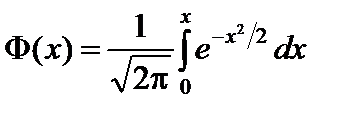. (67)
Вероятность того, что абсолютная величина отклонения меньше положительного числа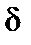 
отражается формулой
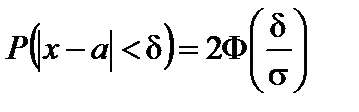. (68)
В частности, при а = 0: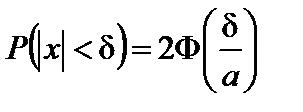 
.
Пусть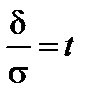 
, 
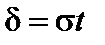. При t = 3, 
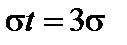, то
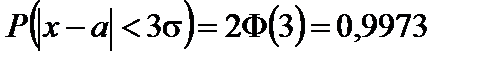. (69)
Полученная формула выражает правило трех сигм.
При a = 0 и s = 1 плотность распределения примет вид:
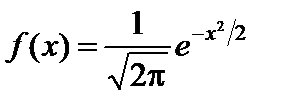. (70)
Распределение вероятностей называется нормированным или стандартным, а график функции – нормированной кривой (рис. 2.10).
Рис. 2.10
Числовые характеристики для нормальной случайной величины Х следующие: M (X) = a, D (X) = s2,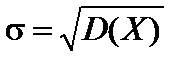 
.
Пример 2.20. Случайная величина X распределена по нормальному закону, причем M (X) = 10. Найти P (0 < X < 10), если известно, что P (10 < X < 20) = 0,3.
Решение. По условию a = M (X) = 10.
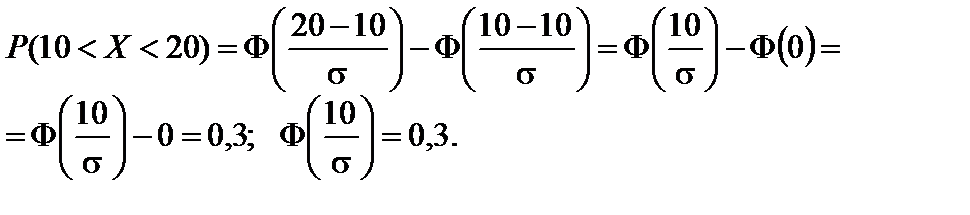
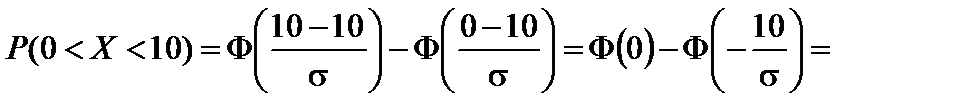
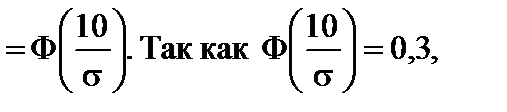следовательно 
.
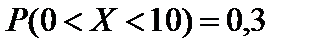Пример 2.21. Вес пойманной рыбы подчиняется нормальному закону распределения с параметрами a = 375 г, s = 25 г. Найти вероятность того, что вес одной рыбы будет: а) от 300 до 425 г; б) не более 450 г; в) больше 300 г.
Решение:
а) при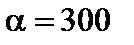 
и b = 425 вероятность равна:
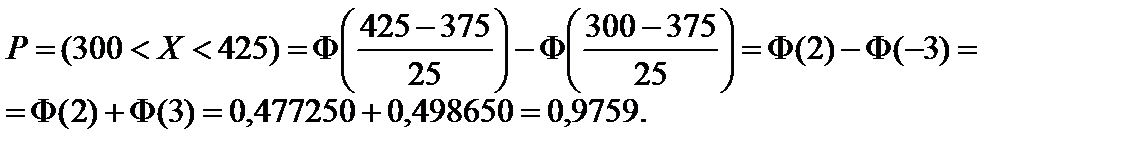
б) при X < 450:
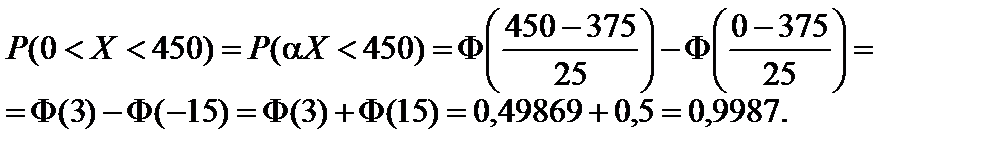
в) при X > 300:
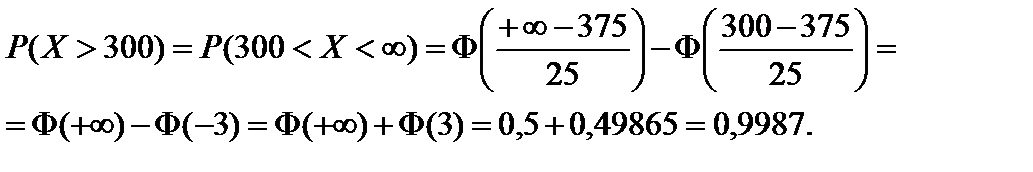
Пример 2.22. При измерении детали получаются случайные ошибки, подчиненные нормальному закону со средним квадратическим отклонением, равным 10 мм. Какова вероятность того, что измерение произведено с ошибкой, не превосходящей 15 мм?
Решение. Для расчета используем формулу (68) с учетом того, что по условию d = 15 и s = 10.
.
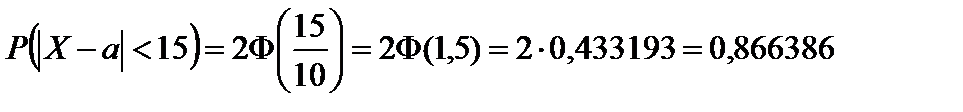Пример 2.23. Автомат изготавливает подшипники, которые считаются годными, если отклонение X от проектного размера по модулю не превышает 0,77 мм. Каково наиболее вероятное число годных подшипников из 100, если случайная величина X распределена нормально с параметром s = 0,4 мм?
Решение. По условию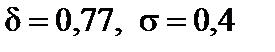 
.
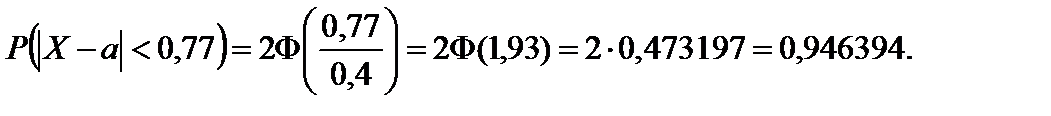
Считая приближенно p = 0,95 и q = 0,05, в соответствии с неравенством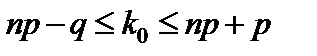 
, при n = 100 находим:
; 
.
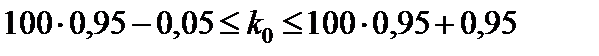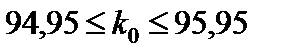Отсюда k 0 = 95.
Пример 2.24. Станок-автомат изготавливает валики, контролируя их диаметры X. Случайная величина X распределена нормально, с параметрами a = 10 мм, s = 0,1 мм. Найти интервал, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных валиков.
Решение.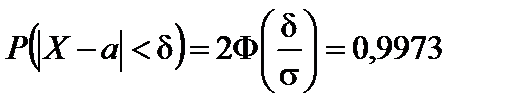 
, требуется найти интервал 
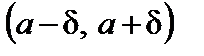. По таблице значений функции Лапласа находим, что 
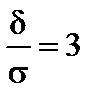, это вытекает из равенства 
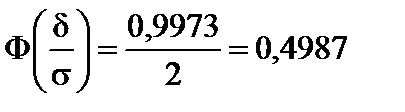, d = 3s =
= 3 · 0,1 = 0,3.
Из неравенства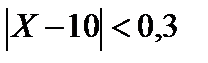 
получаем следующее:
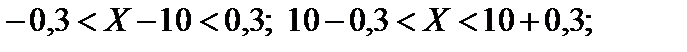
Следовательно, искомый интервал: 9,7 < X < 10,3.
Пример 2.25. Линия связи обслуживает 1000 абонентов. Каждый абонент разговаривает в среднем 6 минут в час. Сколько каналов должна иметь линия связи, чтобы с практической достоверностью можно было утверждать, что не произойдет ни одной потери вызова?
Решение. Вероятность вызова для каждого абонента равна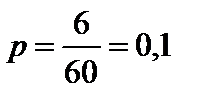 
, q = 1 – p = 0,9, поэтому a = np = 1000 · 0,1, s =
= 
.
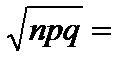
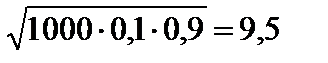Согласно формуле (69), практически достоверно, что
.
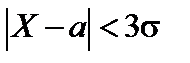Отсюда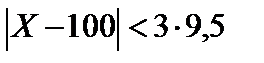 
; 
; 
.
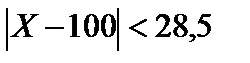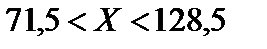Для практически безотказной работы линии связи достаточно иметь 130 каналов.
