Показательным распределением называется распределение с плотностью вероятностей, определяемой следующей функцией:
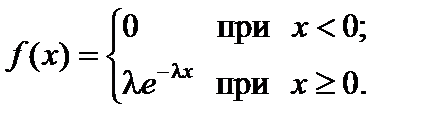 (71)
(71)
График функции f (x) изображен на рис. 2.11.

Рис. 2.11
Функция распределения показательного закона:
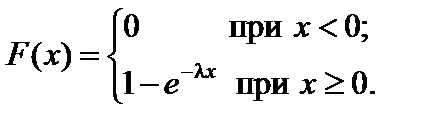 (72)
(72)
Вероятность попадания в интервал (a; b) равна:
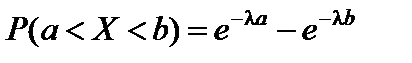 . (73)
. (73)
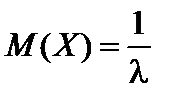 ;
; 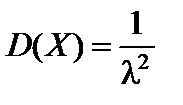 ;
; 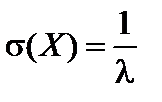 .
.
Пример 2.26. Написать плотность распределения и функцию распределения показательного закона, если l = 7.
Решение.
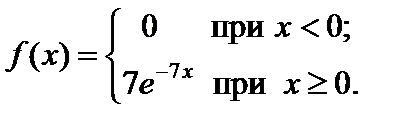
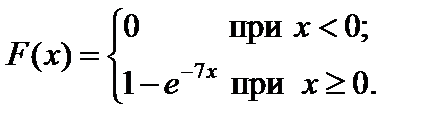
Пример 2.27. Какова вероятность того, что в результате испытания непрерывная случайная величина X попадет в интервал (0,3; 1), если она распределена по показательному закону 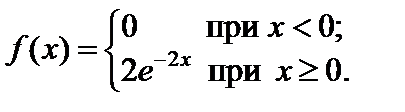
Решение. По условию 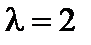 , следовательно:
, следовательно:
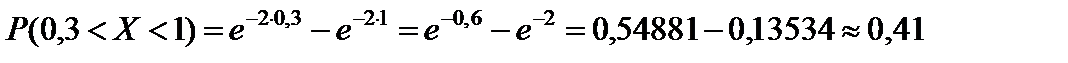 .
.
 2015-04-20
2015-04-20 857
857








