Распределение вероятностей случайной величины X называется равномерным на отрезке [ a; b ], если плотность вероятностей этой величины постоянна на данном отрезке и равно нулю вне этого отрезка.
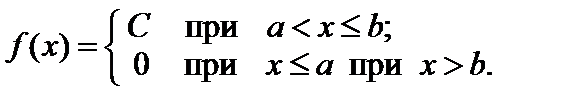
Найдем значение C: 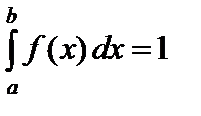 или
или 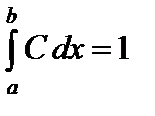 .
.
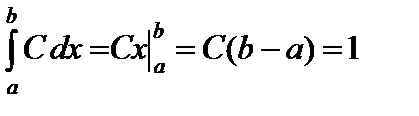 ;
; 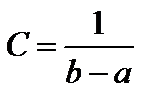 .
.
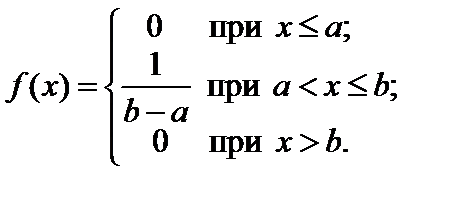 (63)
(63)
Найдем интегральную функцию F (x) случайной величины X, имеющей равномерное распределение, используя формулу (52).
Если 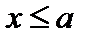 , то f (x) = 0, следовательно, F (x) = 0.
, то f (x) = 0, следовательно, F (x) = 0.
Если 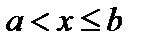 , то
, то 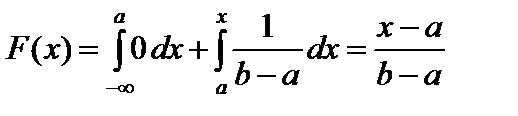 .
.
Если 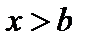 , то
, то 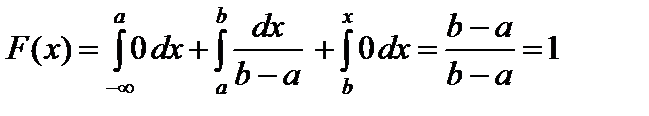 .
.
Интегральная функция распределения имеет вид:
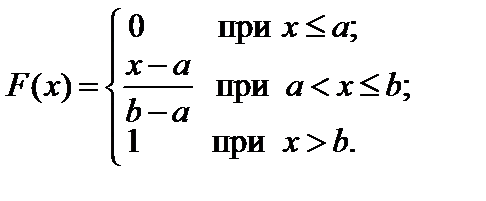 (64)
(64)
Графики функций F (x) и f (x) представлены на рис. 2.7 и 2.8.
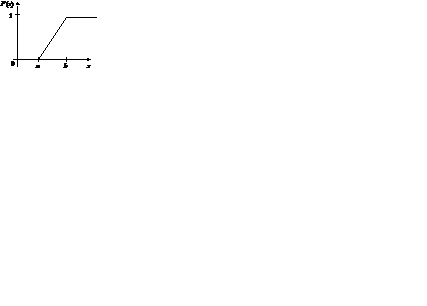 Рис. 2.7 Рис. 2.7 | 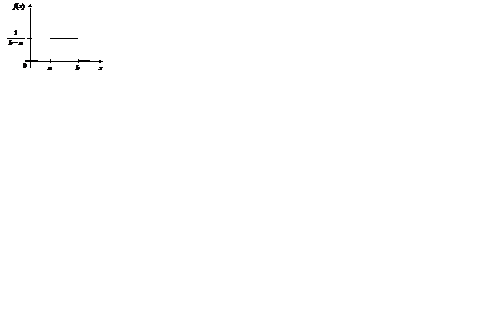 Рис. 2.8 Рис. 2.8 |
Пример 2.18. Найти математическое ожидание и дисперсию случайной величины X, имеющей равномерное распределение на отрезке [ a; b ].
Решение.
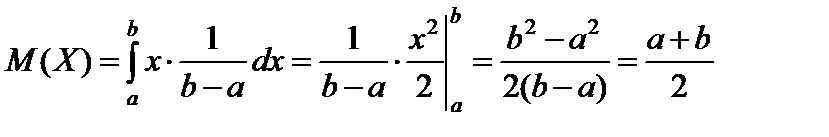 ;
;
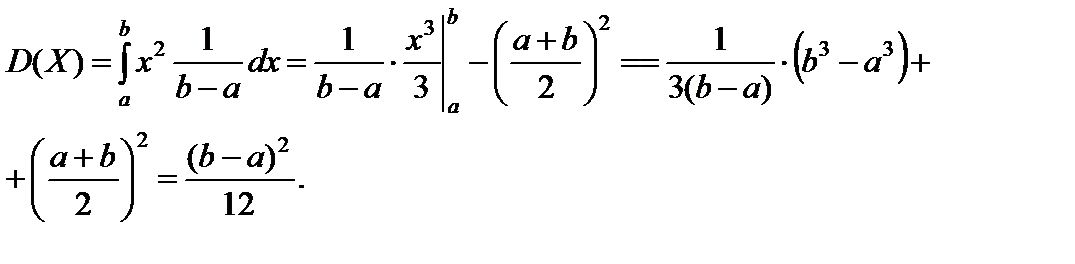
Следовательно, 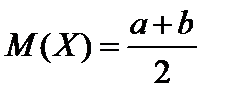 ;
; 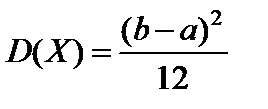 .
.
Пример 2.19. Найти вероятность того, что случайная величина X, распределенная равномерно в интервале (2; 8), примет значение, принадлежащее интервалу (5; 7).
Решение. Для равномерного распределения
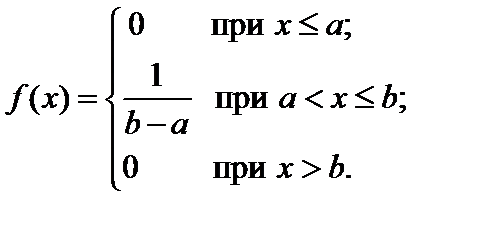 или
или 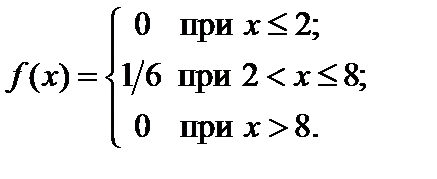
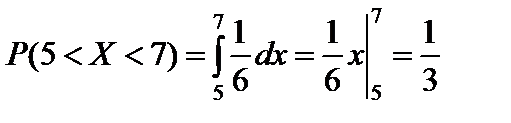 .
.
 2015-04-20
2015-04-20 734
734








