1. После составления исходной матрицы данных для каждого признака находятся средние арифметические 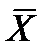 и
и 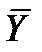 .
.
2. Для дальнейших расчетов целесообразно воспользоваться таблицей следующего вида:
Таблица 21
| № | xi | yi | xi– 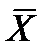 | yi– 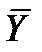 | (xi– 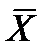 )2 )2 | (yi– 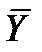 )2 )2 | (xi– 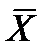 )*(yi– )*(yi– 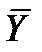 ) ) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| … | |||||||
| N | |||||||
| å | å=……… | å=…….. | å=……………… |
В столбцы 2 и 3 занесены первичные данные.
3. Для каждого значения переменной xi находим разность xi– 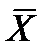 и записываем в столбик 4.
и записываем в столбик 4.
4. Для каждого значения переменной y iнаходим разность yi– 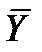 и записываем в столбик 5.
и записываем в столбик 5.
5. В каждой строчке таблицы полученные разности возводим в квадрат и записываем в столбики 6 и 7.
6. Квадраты разностей, записанные в столбике 6, сложить.
7. Аналогично найти сумму квадратов разностей по столбику 7.
8. В каждой строчке таблицы находим произведение разностей (xi– 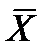 )*(yi–
)*(yi– 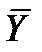 ) и записываем в столбик 8.
) и записываем в столбик 8.
9. Находим сумму полученных произведений.
10. Вычисленные суммы (по столбикам 6, 7 и 8) подставить в формулу и вычислить расчетное значение коэффициента линейной корреляции Пирсона.
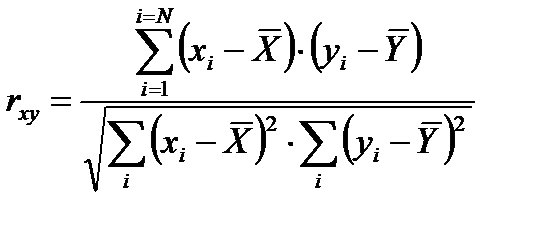
11. Правило вывода: Определить по таблице (см. таблицу критических значений коэффициента линейной корреляции Пирсона) критическое значение rxy для данного N.
Если rxy расч.≥rxy критич., корреляция достоверно отличается от 0, т.е. взаимосвязь между признаками статистически значима.
Если rxy расч.< rxy критич., корреляция недостоверно отличается от 0, т.е. взаимосвязь между признаками отсутствует.
Расчеты коэффициента корреляции Пирсона довольно трудоемки, поэтому для обработки реальных данных чаще всего пользуются компьютерными программами.
Корреляционное отношение — мера нелинейной (криволинейной) взаимосвязи между признаками, измеренными по количественным шкалам (интервальной или пропорциональной). Алгоритм его расчета можно найти в случае необходимости в учебнике Ермолаева О. Ю. Математическая статистика для психологов. — М., 2008.
Контрольные вопросы:
1. Что такое стохастическая зависимость?
2. Какими свойствами обладают связи между признаками?
3. Приведите общее правило вывода при оценке взаимозависимостей между признаками.
4. Какая мера связи пригодна для оценки зависимостей между признаками, измеренными по шкале наименований?
5. Какие меры связи пригодны для оценки зависимостей между признаками, измеренными по шкале наименований и шкале порядка?
6. Какие меры связи пригодны для оценки зависимостей между признаками, измеренными по шкале наименований и какой-либо количественной шкале (интервальной или пропорциональной)?
7. Какая мера связи пригодна для оценки зависимостей между признаками, измеренными по шкале порядка?
8. Какая мера связи пригодна для оценки зависимостей между признаками, измеренными по шкале порядка и какой-либо количественной шкале (интервальной или пропорциональной)?
9. Какая мера связи пригодна для оценки зависимостей между признаками, измеренными по шкале какой-либо количественной шкале (интервальной или пропорциональной)?
10. В каком случае более адекватной мерой является корреляционное отношение и для каких шкал оно применяется?
Самостоятельное практическое задание:
Решите примеры.
1. Проранжируйте 50 оценок рефлексивности испытуемых: 134 125 126 124 126 121 109 125 143 106 134 103 128 131 141 127 125 103 117 107 133 111 127 122 147 125 140 137 118 114 120 121 122 121 111 135 129 116 124 120 93 100 117 129 112 111 116 120 102 139
2. На основе приведенных данных (таблица 22) определить, влияет ли на отчисление студентов из ВУЗа их семейное положение.
Х — семейное положение: 0 — неженат, незамужем; 1 — женат, замужем.
У — «пребывание» в ВУЗе: 0 — исключен, 1 — учится.
Таблица 22
| № п/п | ||||||||||||
| Хi | ||||||||||||
| Уi |
2. Установить, существует ли взаимосвязь между полом и вербальными способностями (или иначе есть ли гендерные различия в развитии вербальных способностей). В таблице 23 с первичными данными: пол обозначен следующим образом: 1 — юноши, 2 — девушки; оценки вербальных способностей — сумма первичных баллов по методике.
Таблица 23
| № п/п | Пол | Вербальные способности |
3. Рассчитайте поправки для различных случаев связанных рангов: а=2; а=3; а=4; а=5 и а=6.
4. Определите, существует ли сходство в выраженности акцентуируемых черт личности матери и 8-летнего сына. Выраженность черт оценивалась с помощью методики Шмишека, в таблице 24 представлены «сырые» оценки (первичные баллы) по методике.
Таблица 24
| Черты личности | Мать | Сын |
| Застреваемость | ||
| Педантичность | ||
| Гипертимность | ||
| Демонстративность | ||
| Тревожность | ||
| Эмотивность | ||
| Дистимность | ||
| Возбудимость | ||
| Экзальтированность | ||
| Лабильность |
Материалы для изучения:
а) основная литература:
1. Ермолаев О. Ю. Математическая статистика для психологов [Текст]: учебник / О. Ю. Ермолаев. - 5-е изд. - М.: МПСИ: Флинта, 2011. - 336 с. - С. 202-254.
2. Наследов А.Д. Математические методы психологического исследования: Анализ и интерпретация данных [Текст]: учебное пособие / А. Д. Наследов. - 3-е изд., стереотип. - СПб.: Речь, 2007. - 392 с. - С. 147-161.
3. Сидоренко Е. В. Методы математической обработки в психологии [Текст] / Е. В. Сидоренко. - СПб.: Речь, 2010. - 350 с.: ил. - С. 200-223.
б) дополнительная литература:
1. Гласс Дж. Статистические методы в педагогике и психологии [Текст]. / Дж. Гласс, Дж. Стенли— М., 1976. – 494 с. - С. 103-122.
2. Кутейников А.Н. Математические методы в психологии [Текст]: учебно-методический комплекс / А. Н. Кутейников. - СПб.: Речь, 2008. - 172 с.: табл. - С. 53-80.
3. Суходольский Г.В. Основы математической статистики для психологов [Текст]: учебник / Г. В. Суходольский. - СПб.: Изд-во СПбГУ, 1998. - 464 с. - С. 162-219.
 2015-04-20
2015-04-20 2001
2001
