1. Определить, какие два признака или две иерархии признаков будут участвовать в расчетах. Для удобства расчетов составить таблицу следующего вида:
Таблица 20
| № п/п | X1 | X2 | R X1 | R X2 | di | di2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| …. | ||||||
| N | ||||||
| Σdi2 |
Заполнить в таблице столбцы 2 и 3 первичными данными.
2. Проранжировать значения переменной 1, начисляя ранг 1 наименьшему значению, в соответствии с правилами ранжирования. Занести ранги в столбец 4 таблицы по порядку номеров испытуемых или признаков.
3. Проранжировать значения переменной 2 в соответствии с теми же правилами. Занести ранги в столбец 5 таблицы по порядку номеров испытуемых или признаков.
4. Подсчитать разности рангов в каждой строке таблицы по формуле:
di = R X1 – R X2 и занести их в столбец 6 таблицы.
5. Возвести каждую разность в квадрат. Эти значения занести в столбец 7 таблицы.
6. Подсчитать сумму квадратов разностей Σdi2
7. При наличии одинаковых рангов рассчитать поправки:
Та= Σ(a3–a)/12
Тb= Σ(b3–b)/12
где a — объем каждой группы одинаковых рангов в ранговом ряду R X1 (в столбце 4);
b — объем каждой группы одинаковых рангов в ранговом ряду R X2 (в столбце 5).
8. Рассчитать коэффициент ранговой корреляции ρ по формуле:
а) при отсутствии одинаковых рангов
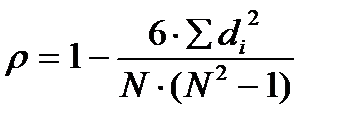

б) при наличии одинаковых рангов
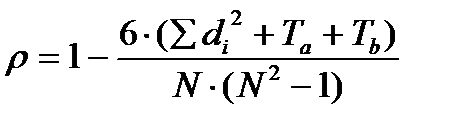
где Σdi2 - сумма квадратов разностей между рангами;
Та и Т b - поправки на одинаковые ранги;
N - количество испытуемых или признаков, которые ранжировались.
9. Правило вывода: Определить по таблице (приложение 3) критическое значение ρ для данного N.
Если ρ превышает критическое значение или по крайней мере равен ему, корреляция достоверно отличается от 0, т.е. взаимосвязь между признаками статистически значима.
Если ρ меньше критического значения, корреляция недостоверно отличается от 0, т.е. взаимосвязь между признаками отсутствует.
Коэффициент ранговой корреляции Кендэлла в лекциях не рассмотрен, так как он применяется значительно реже.
 2015-04-20
2015-04-20 2928
2928
