Предел функции нескольких переменных

Пусть точка 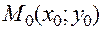является для области определения 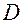функции 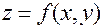внутренней или граничной, так что в любой ее 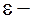окрестности (то есть сколь угодно близко от нее) содержатся точки области .

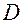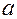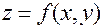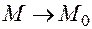Определение. Число называется пределом функции в точке (говорят также: при или при 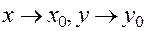), если для любого 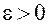(сколь угодно малого) существует 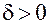, такое что при выполнении условий 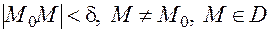справедливо неравенство .

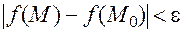Обозначения:

; ; ;

.

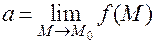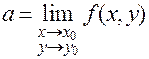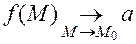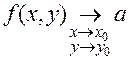Аналогично определяется предел функции трех или более переменных.

Замечания. 1. Геометрически утверждение о том, что 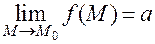, означает, что значения функции 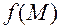сколь угодно близко приближаются к числу 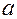, если точка 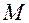, оставаясь в области определения 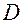, достаточно близко подходит к точке .

2. Предел функции нескольких переменных обладает cвойствами, аналогичными свойствам предела функции одной переменной [1]. Мы будем использовать их по мере необходимости.