Пусть функция 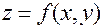 определена в окрестности точки
определена в окрестности точки 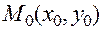 .
.
Определение. Частной производной функции 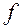 в точке
в точке  по переменной
по переменной 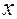 называется предел отношения частного приращения
называется предел отношения частного приращения 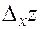 в этой точке к вызвавшему его приращению
в этой точке к вызвавшему его приращению 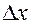 переменной
переменной 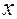 при
при 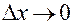 .
.
Обозначения частной производной:
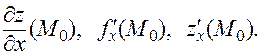
Итак, согласно определению,
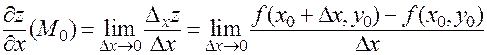 .
.
Аналогично
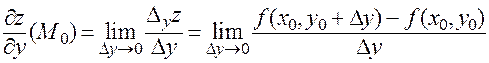 .
.
Таким же образом определяются частные производные для функции большего числа переменных. Например, для функции 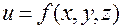 :
:
 .
.
При вычислении частной производной по переменной 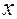 все остальные независимые переменные считают постоянными величинами (равными соответствующим координатам точки
все остальные независимые переменные считают постоянными величинами (равными соответствующим координатам точки  ), и применяют правила дифференцирования функции одной переменной [4].
), и применяют правила дифференцирования функции одной переменной [4].
Примеры. 1. 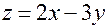 .
.
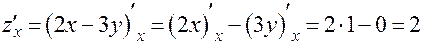
(производная второго слагаемого равна нулю как производная константы);
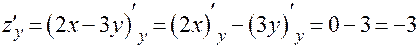 .
.
2.  .
.
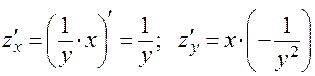 .
.
3. 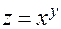 . Частная производная по переменной
. Частная производная по переменной 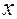 является производной степенной функции с фиксированным показателем
является производной степенной функции с фиксированным показателем 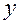 ; поэтому
; поэтому 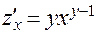 . Частная производная по переменной
. Частная производная по переменной 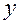 является производной показательной функции с фиксированным основанием
является производной показательной функции с фиксированным основанием 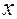 ; поэтому
; поэтому 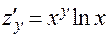 .
.
4. 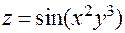 . По правилу дифференцирования сложной функции:
. По правилу дифференцирования сложной функции:
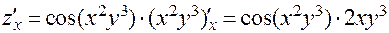 ;
;
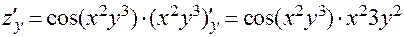 .
.
5.  .
.
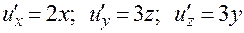 .
.
6. 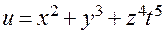 .
.
 .
.
 2015-05-14
2015-05-14 855
855








