Пусть 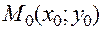 ― фиксированная точка области определения
― фиксированная точка области определения 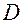 функции
функции 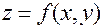 , а приращения
, а приращения 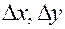 независимых переменных
независимых переменных 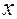 и
и 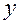 не выводят переменные точки
не выводят переменные точки
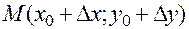 ,
, 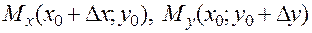
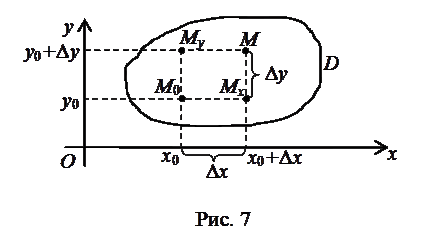
за пределы 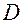 (рис. 7).
(рис. 7).
 |
Определение. 1. Полным приращением функции
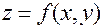 в точке
в точке  называется разность
называется разность 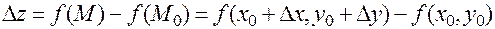 .
.
Для фиксированной точки  полное приращение
полное приращение 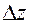 является функцией переменных
является функцией переменных 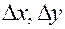 , которая определена при всех достаточно малых по модулю
, которая определена при всех достаточно малых по модулю 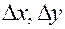 .
.
2. Частным приращением функции 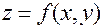 в точке
в точке  по переменной
по переменной 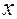 называется разность
называется разность
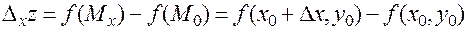 .
.
Для фиксированной точки  частное приращение
частное приращение 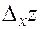 является функцией переменной
является функцией переменной 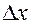 , которая определена при всех достаточно малых по модулю
, которая определена при всех достаточно малых по модулю 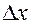 .
.
Аналогично частным приращением функции 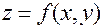 в точке
в точке  по переменной
по переменной 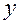 называется разность
называется разность
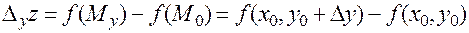 .
.
Для фиксированной точки  частное приращение
частное приращение 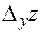 является функцией переменной
является функцией переменной 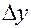 , которая определена при всех достаточно малых по модулю
, которая определена при всех достаточно малых по модулю 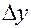 .
.
Пример. Рассмотрим функцию 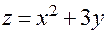 . Ее полное приращение
. Ее полное приращение
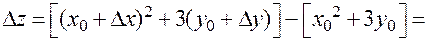
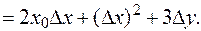
Частные приращения:
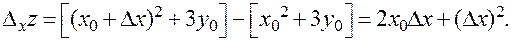
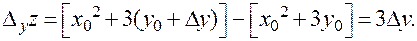
Если 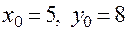 , то в точке
, то в точке 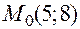 :
:
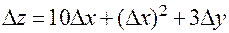 ;
; 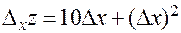 ;
; 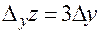 .
.
Аналогично определяются полное и частные приращения функции большего числа переменных. Например, для функции 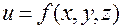 :
:
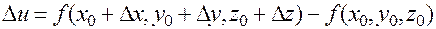 ;
;
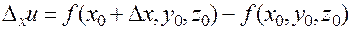 ;
;
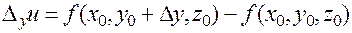 ;
;
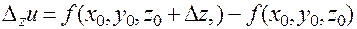 .
.
 2015-05-14
2015-05-14 3997
3997
