Вывод формулы парабол (Симпсона)

Пусть дана криволинейная трапеция, ограниченная функциями y = f (x), x = a, x = b, y = 0.

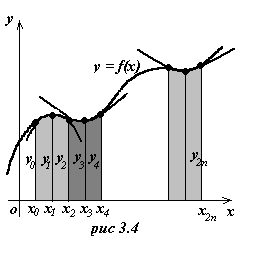
1. Разобьем отрезок [a; b] на 2п равных частей. Получим отрезки длиной 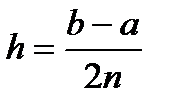(9)
2. В точках деления вычислим значения функции

y = f (x): у₀, у₁, у₂,......, у_2п-2, у_2п-1, у_2п.

1. Заменим каждую пару соседних криволинейных трапеций параболическими трапециями с основаниями, равными 2h.

На отрезке [ x₀; x₂ ] парабола проходит через точки (х₀; у₀), (х₁; у₁), (х₂; у₂).

Используя формулу (8) получим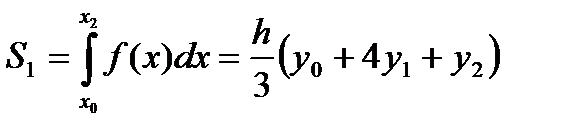

Аналогично на отрезке [ x₂; x₄ ]: 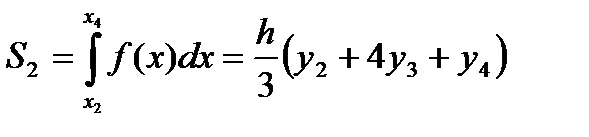и т. д. до

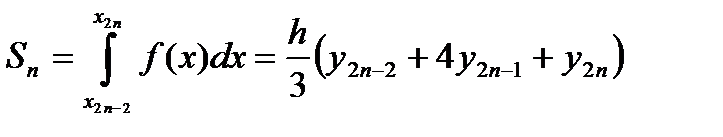
Следовательно:

=

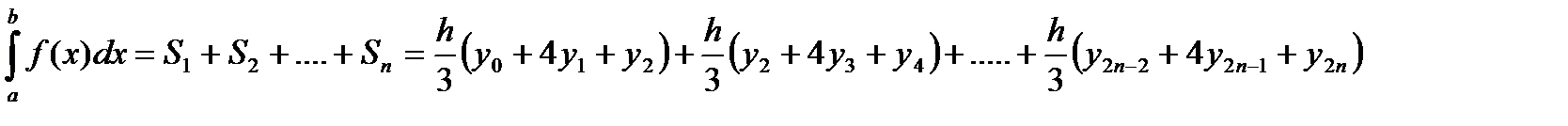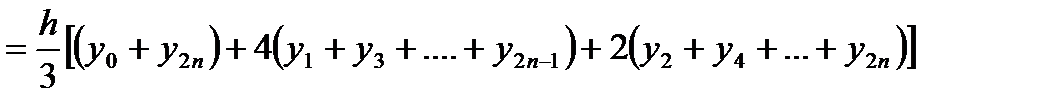
Учитывая погрешность вычислени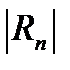й и 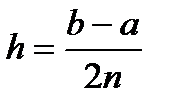, получим формулу Симпсона

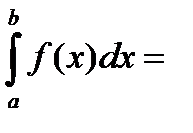
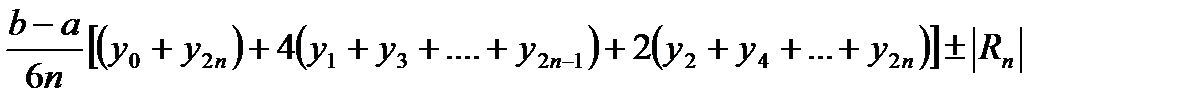(10)

Абсолютная погрешность метода оценивается соотношением:

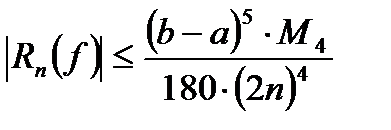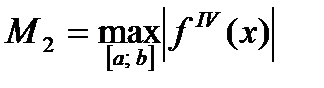где (11)

Пример 3.4:

Вычислить интеграл 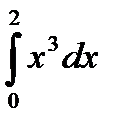, используя метод парабол при п = 4.