Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.
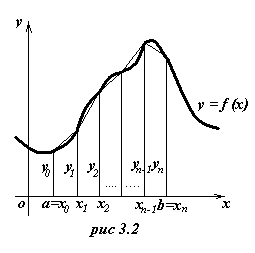 Пусть на отрезке [a; b], где a < b, задана непрерывная функция f(x). Требуется вычислить интеграл
Пусть на отрезке [a; b], где a < b, задана непрерывная функция f(x). Требуется вычислить интеграл 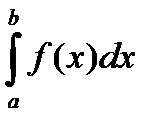 , численно равный площади соответствующей криволинейной трапеции. Разобьем основание этой трапеции на п равных частей длины
, численно равный площади соответствующей криволинейной трапеции. Разобьем основание этой трапеции на п равных частей длины 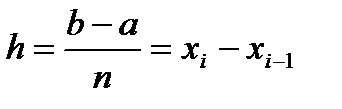 . тогда xi = x0+hi, yi = f (xi).
. тогда xi = x0+hi, yi = f (xi).
Так как площадь криволинейной трапеции приблизительно равна сумме площадей трапеций Si, высота каждой из которых равна h, то:
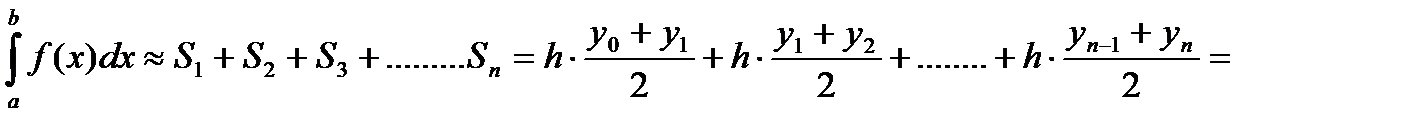
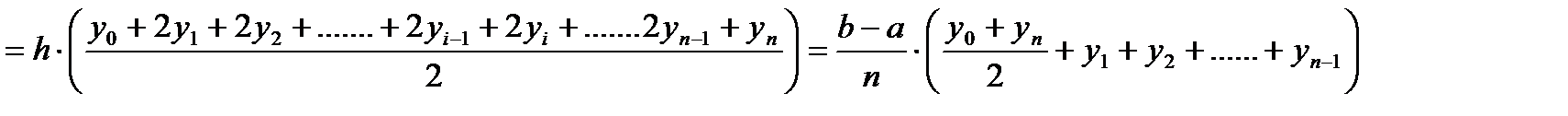
Абсолютная погрешность метода (аналогично методу прямоугольников) составляет:
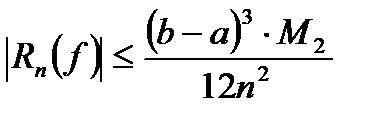 где
где 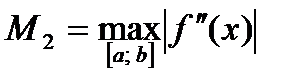 (4)
(4)
тогда 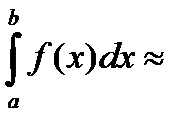
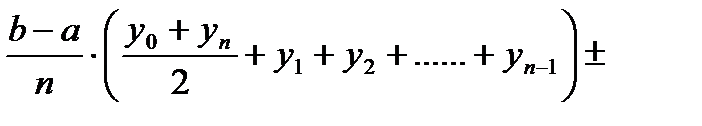
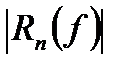 - формула трапеций. (5)
- формула трапеций. (5)
Пример 3.3: Вычислить интеграл 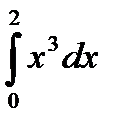 при п = 4, используя метод трапеций.
при п = 4, используя метод трапеций.
Решение. По формуле трапеций:
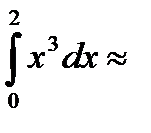
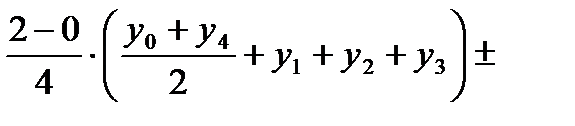
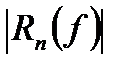 , т.к.
, т.к. 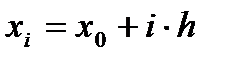 ,
, 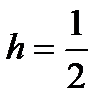 , то
, то
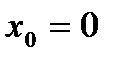 ,
, 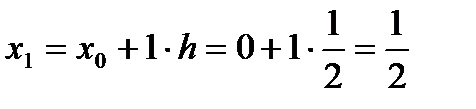 ,
, 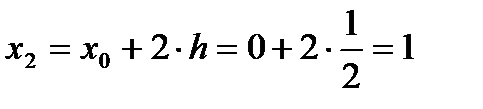 ,
, 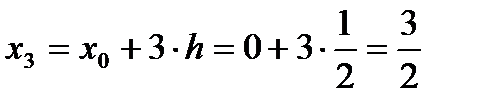 ,
, 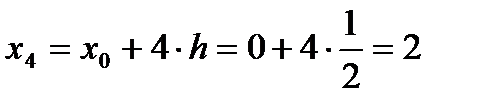 .
.
Тогда 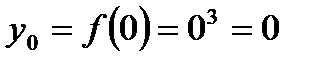 ,
, 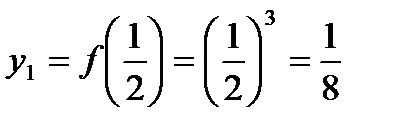 ,
, 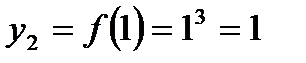 ,
, 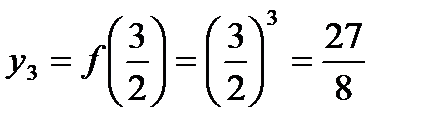 ,
, 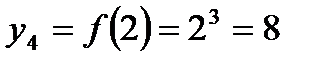 .
.
Найдем погрешность:
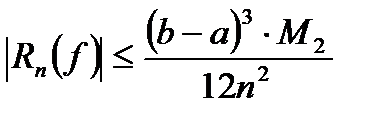 где
где 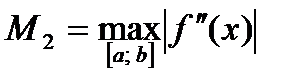
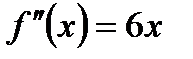 ,
, 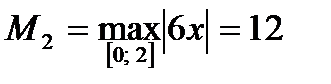 ,
, 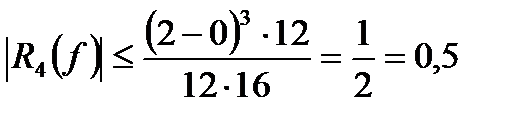
Следовательно
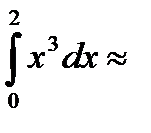
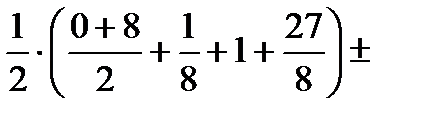
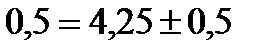
 2015-05-14
2015-05-14 770
770








