Общее решение однородной линейной системы

Рассмотрим однородную линейную систему

(6)

Очевидно, что такая система всегда совместна, поскольку имеет нулевое решение 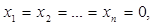называемое тривиальным.

Матрицей системы (6) называется матрица вида

. (7)

Пусть ранг матрицы системы r < n. Неизвестные 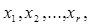коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные (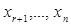) – свободными неизвестными.

Тогда число линейно независимых решений системы (6) равно n – r. При этом любые n – r линейно независимых решений системы (6) называются ее фундаментальной системой решений, а любое решение однородной линейной системы (6) является линейной комбинацией фундаментальной системы ее решений, то есть 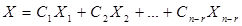, где - фундаментальная система решений.