Пример 17

Найти общее решение и одно из частных решений линейной системы

.

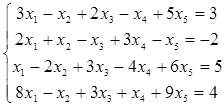Решение.

Найдем r (A) и r (A ₁):

~ ~

~ ~ ~

~ .

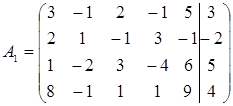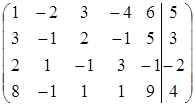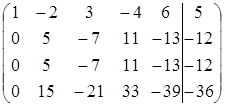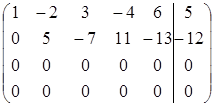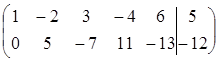Итак, r = r (A) = r (A ₁) = 2, а число неизвестных п = 5. Следовательно, r < n, и система имеет бесконечно много решений (совместна, но не определена).

Число базисных неизвестных равно r, то есть двум. Выберем в качестве базисных неизвестных х ₁ и х ₂, коэффициенты при которых входят в базисный минор преобразованной матрицы А: .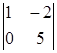

Соответственно х ₃, х ₄, х ₅ – свободные неизвестные.

Запишем систему, равносильную исходной, коэффициентами в которой являются элементы полученной матрицы:

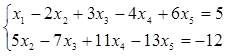
и выразим базисные неизвестные через свободные:

.

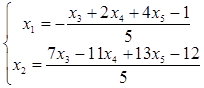Получено общее решение системы. Одно из частных решений можно найти, положив все свободные неизвестные равными нулю: х ₃ = х ₄ = х ₅ = 0. Тогда

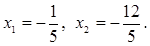
Таким образом, общее решение – ;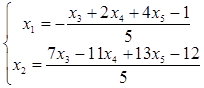

частное решение – 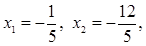х ₃ = х ₄ = х ₅ = 0.

Другая возможность получить общее решение неоднородной системы заключается в предварительном нахождении общего решения соответствую-щей однородной системы. При этом искомое общее решение представляет собой сумму общего решения соответствующей однородной системы (6) и частного решения системы (3).