Пример 16

Найти фундаментальную систему решений однородной линейной системы

.

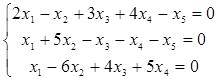Решение.

Найдем r (A):

~ ~ ~

~ .

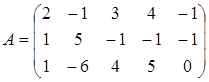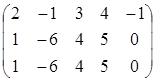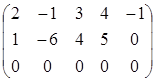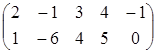Выберем в качестве базисного минора .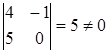

Значит, r (A) = 2. Пусть х ₄, х ₅ – базисные неизвестные, х ₁, х ₂, х ₃ – свободные неизвестные. Запишем для них новую систему:

,

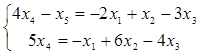откуда .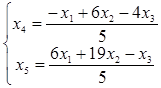

Фундаментальная система решений состоит из трех столбцов. Рассмотрим три набора значений свободных неизвестных:

1) х ₁ = 1, х ₂ = х ₃ = 0.

Тогда х ₄ = -0,2, х ₅ = 1,2, и решение можно записать в виде столбца .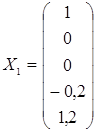

2) х ₁ = 0, х ₂ = 1, х ₃ = 0.

При этом х ₄ = 1,2, х ₅ = 3,8, и следующее решение системы имеет вид .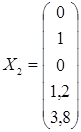

3) х ₁ = х ₂ = 0, х ₃ = 1. Отсюда х ₄ = -0,8, х ₅ = -0,2, и последний столбец

.

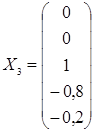Фундаментальная система решений, построенная при таком выборе свободных неизвестных, называется нормальной. Поскольку столбцы свободных неизвестных 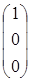, , 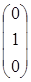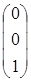линейно независимы, это гарантирует линейную независимость решений Х ₁, Х ₂, Х ₃.

Итак, в качестве фундаментальной системы решений можно выбрать

, , .

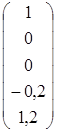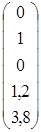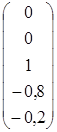При этом любое решение данной системы имеет вид: Х = с ₁ Х ₁ + с ₂ Х ₂ + с ₃ Х ₃, где с ₁, с ₂, с ₃ – произвольные постоянные. Эта формула задает общее решение системы.