2015-05-14
460
Решить систему по правилу Крамера:
.
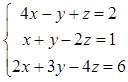Решение.
Главный определитель
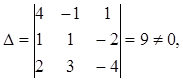
следовательно, система имеет единственное решение.
Найдем Δ х, Δ у и Δ z:
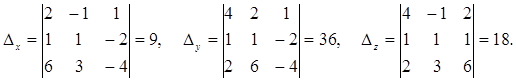
Отсюда
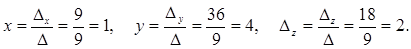
Решение линейных систем с помощью обратной матрицы
Рассмотрим линейную систему (3) и введем следующие обозначения:
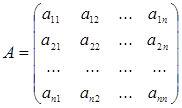- матрица системы, 
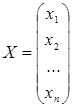- столбец неизвестных,
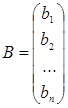- столбец свободных членов. Тогда систему (3) можно записать в виде матричного уравнения: АХ = В. (5)
Пусть матрица А – невырожденная, тогда существует обратная к ней матрица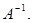 
Умножим обе части равенства (5) слева на 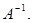Получим
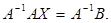
Но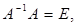 
тогда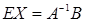 
, а поскольку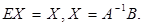 
Итак,решением матричного уравнения (5) является произведение матрицы, обратной к А, на столбец свободных членов системы (3).
