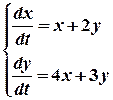
Решение:
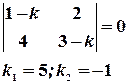
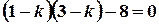 ;
; 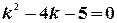
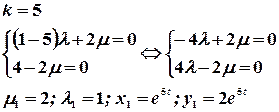
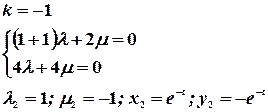
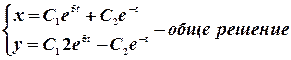
2.2. Корни характеристического уравнения действительные и равные.
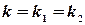 решение усложняется за счет алгебраических преобразований.
решение усложняется за счет алгебраических преобразований.
Решение ищут в виде
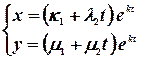 подставляют их в одно уравнение системы и используя метод неопределенных коэффициентов. Находят коэффициенты
подставляют их в одно уравнение системы и используя метод неопределенных коэффициентов. Находят коэффициенты 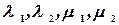 , или считают
, или считают 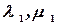 произвольными числами, а
произвольными числами, а 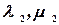 находят в зависимости от них.
находят в зависимости от них.
2.3. Корни характеристического уравнения комплексные 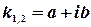 . Этим корням соответствуют решения
. Этим корням соответствуют решения
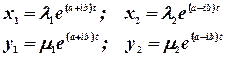
Где 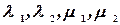 определяются из системы (7).
определяются из системы (7).
Можно показать, что для системы, как и для аналогичного случая характеристического уравнения однородного линейного уравнения 2 – го порядка действительная и мнимая части комплексного решения также являются решениями, т. е. получают частные решения в виде:
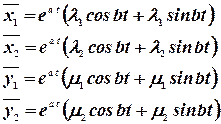
Можно было найдя 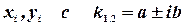 сразу написать общее решение в виде
сразу написать общее решение в виде 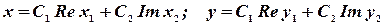 .
.
 2015-05-14
2015-05-14 249
249








