Познакомимся с более удобной формой записи системы линейных дифференциальных уравнений и ее решений.
Пусть дана нормальная система однородных линейных дифференциальных уравнений.
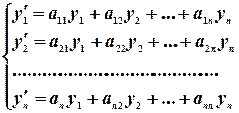 | (9) |
Составим матрицу из коэффициентов системы.
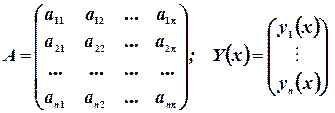 - матрица – столбец неизвестных функций (или вектор-функция скалярного аргумента)
- матрица – столбец неизвестных функций (или вектор-функция скалярного аргумента)
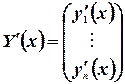
Тогда систему (9) коротко можно записать как матричное дифференциальное уравнение
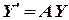 или или 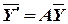 | (10) |
Частными решениями (10) является вектор – функция (векторы 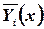 с координатами
с координатами 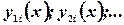 )
) 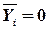 - тривиальное решение.
- тривиальное решение.
Зная правила действия с матрицами, легко проверить, что любая линейная комбинация частных решений 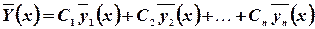 тоже решение (10).
тоже решение (10).
Замечание: функции 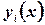 - линейно независимы.
- линейно независимы.
Известна теорема.
Т.3.1. Для того чтобы решения 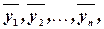 были линейно независимы, необходимо и
были линейно независимы, необходимо и
достаточно, чтобы определитель 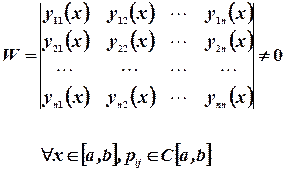 был отличен от нуля.
был отличен от нуля.
О.3.1. Любая линейно независимая система 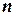 решений называется фундаментальной системой, а определитель
решений называется фундаментальной системой, а определитель 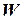 - определителем Вронского.
- определителем Вронского.
По аналогии с дифференциальными уравнениями; если фундаментальная система известна, то общее решение 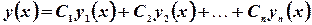 - линейная комбинация частных решений.
- линейная комбинация частных решений.
|
|
|
Если система с постоянными коэффициентами, то частные решения (см. выше) отыскиваются в виде 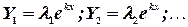
Вектор – функции 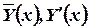 запишутся так
запишутся так
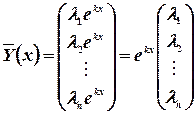 ;
; 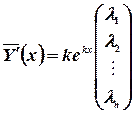
Пусть
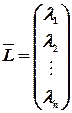 |
Тогда (10) перепишем в виде
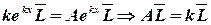 | (11) |
– матричное алгебраическое уравнение
При 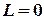 - имеем тривиальное решение. Найдем
- имеем тривиальное решение. Найдем 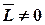 , чтобы
, чтобы 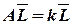 , где вектор
, где вектор 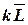 коллинеарен
коллинеарен 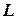 .
.
О.3.2. Числа 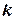 ,при которых существует ненулевое решение (11) называются собственными числами, а векторы
,при которых существует ненулевое решение (11) называются собственными числами, а векторы 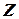 собственными векторами матрицы.
собственными векторами матрицы.
Замечание: Если 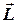 собственный вектор, соответствующий собственному числу
собственный вектор, соответствующий собственному числу 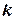 , то и любой вектор
, то и любой вектор 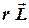 , ему коллинеарный тоже собственный.
, ему коллинеарный тоже собственный.
Т. е. умножая каждое решение на постоянное число, получим снова решение.
 2015-05-14
2015-05-14 2045
2045
