Системы линейных дифференциальных уравнений с постоянными
О.1.1. Системой дифференциальных уравнений называется совокупность уравнений, в каждое из которых входят: неизвестная переменная, искомые функции и их производные. (число уравнений равно числу неизвестных функций).
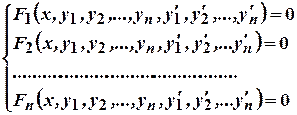
| (1) |
О.1.2. Решением системы (1) называется система из n функций 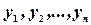 , подстановка которых в уравнения (1) обращает их в тождество.
, подстановка которых в уравнения (1) обращает их в тождество.
О.1.3. Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестной функции, называется нормальной системой.
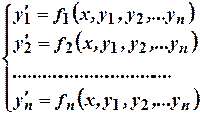
| (2) |
Эта система как обобщение одного дифференциального уравнения первого порядка, разрешенного относительно производной 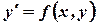 . Известно, что решение такого уравнения
. Известно, что решение такого уравнения 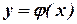 - интегральная кривая уравнения в плоскости
- интегральная кривая уравнения в плоскости 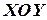 .
.
Замечание: Нормальная система дифференциальных уравнений может быть заменена одним дифференциальным уравнением, порядок которого равен числу уравнений (вспомнить уравнения, сводящиеся к системе).
Если n >2, то решение нормальной системы (2) 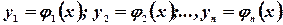 - интегральная кривая в
- интегральная кривая в 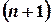 мерном пространстве переменных
мерном пространстве переменных 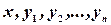 .
.
Начальные условия системы (2) задаются в виде:
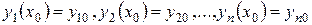
| (3) |
Т.е. ищется интегральная кривая, проходящая через точку 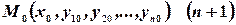 мерного пространства.
мерного пространства.
Постановка задачи Коши: Найти решение системы (1), удовлетворяющее начальным условиям (3).
Теорема Коши: если в некоторой области D 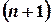 мерного пространства правые части (2) непрерывны вместе со своими частными производными по
мерного пространства правые части (2) непрерывны вместе со своими частными производными по 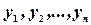 , то существует единственное решение системы, удовлетворяющее заданным начальным условиям.
, то существует единственное решение системы, удовлетворяющее заданным начальным условиям.
О. 1.4. Функции 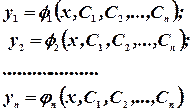
называются общим решением системы (2).
О.1.5. Решения, получающиеся из общего при конкретных значениях 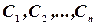 , называются частными решениями (2).
, называются частными решениями (2).
О.2.1. Нормальная система дифференциальных уравнений (2) называется линейной, если функции 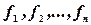 - линейны относительно неизвестных функций
- линейны относительно неизвестных функций 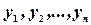 .
.
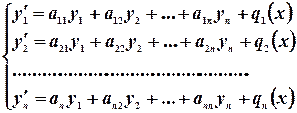
| (4) |
Или 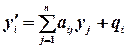 . При
. При 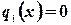 система (4) называется линейной однородной
система (4) называется линейной однородной 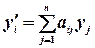 .
.
Так же как и для линейных уравнений высших порядков, существует хорошо разработанная теория линейных однородных и неоднородных систем, изучающая свойства решений, структуру общих решений, метод вариации произвольных постоянных для неоднородных линейных систем и т. д.
Рассмотрим линейную однородную систему дифференциальных уравнений с постоянными коэффициентами. Для простоты пусть 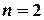 .
.
 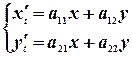
| (5) |
Неизвестные функции 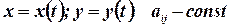
Решения системы (5) обладают следующими свойствами:
1) если 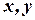 решения (5), то
решения (5), то 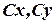 - тоже решения.
- тоже решения.
2) если 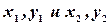 решения (5), то и
решения (5), то и 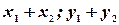 тоже решения (5).
тоже решения (5).
Следствие 1: Если известны два решения системы (5) 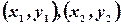 , то
, то 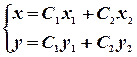 - общее решение (5).
- общее решение (5).
Это справедливо и для линейной однородной системы с непостоянными коэффициентами 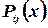 .
.
Итак, рассмотрим систему (5) линейных однородных дифференциальных уравнений.
Будем искать решения в виде
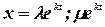
| (6) способ Эйлера |
Где 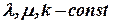 , удовлетворяющие (5).
, удовлетворяющие (5).
Найдем 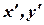 получим
получим
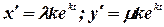
|
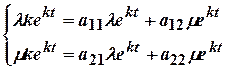
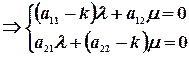 (7)
(7)
Система (7) - однородная алгебраическая система двух уравнений с двумя неизвестными 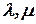 . Чтобы она имела ненулевое решение, необходимо и достаточно чтобы
. Чтобы она имела ненулевое решение, необходимо и достаточно чтобы 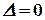 ,следовательно, число
,следовательно, число 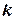 должно удовлетворять условию:
должно удовлетворять условию:
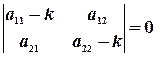
| (8) 
|
Уравнение (8) называется характеристическим уравнением для системы (5).
Его корни называются корнями характеристического уравнения. Т.к. уравнение квадратное, то существуют два корня 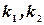 .
.
Рассмотрим различные случаи:
2.1. Корни характеристического уравнения действительные различные 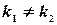 .
.
Если в (7) вместо 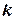 подставить
подставить 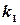 , то решая (7), найдем
, то решая (7), найдем 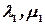 , подставив
, подставив 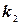 , найдем
, найдем 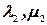 .
.
Т.е. для 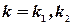 найдем два набора чисел
найдем два набора чисел 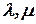 . Соответственно получим две системы частных решений
. Соответственно получим две системы частных решений 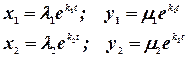
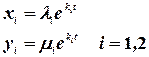 .
.
Тогда общее решение системы имеет вид
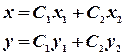 .
.
 2015-05-14
2015-05-14 352
352







