Задача №19. Найти минимум функции

Найти минимум функции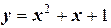

Решение

Функция определена на всей числовой оси. Найдём точки, в которых её производная равна нулю.

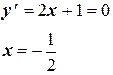
Следовательно область определения функции разбивается на два интервала: 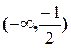и 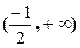. Находим знак производной в каждом интервале:

1) 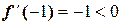, следовательно в интервале 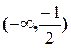функция убывает;

2) 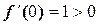, следовательно в интервале 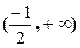функция возрастает.

Таким образом, 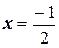является точкой минимума функции. Вычислим значение функции в этой точке:

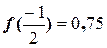
Ответ: 0,75.