Теоремы сравнения рядов

Сходимость или расходимость положительного ряда часто устанавливают путем сравнения его с другим рядом, заведомо сходящимся или расходящимся. В основе такого сравнения лежит следующая теорема.

Теорема 1. Пусть даны два положительных ряда

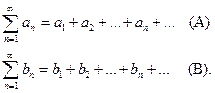
Если, хотя бы начиная с некоторого места (скажем, для n>N), выполняется неравенство: а_nb_n, то из сходимости ряда (В) вытекает сходимость ряда (А) или - что то же - из расходимости ряда (А) следует расходимость ряда (В).

Доказательство. На основании того, что отбрасывание конечного числа начальных членов ряда не отражается на его поведении, мы можем считать, не нарушая общности, что а_nb_n при всех значениях n=1,2,3,... Обозначив частичные суммы рядов (А) и (В), соответственно, через А_n и В_n, будем иметь: а_nb_n.

Пусть ряд (В) сходится, тогда его частичные суммы В_n ограничены: В_nL (L=const; n=1,2,3,...).

В силу предыдущего неравенства, и подавно А_nL, а это, по той же теореме, влечет за собой сходимость ряда (А).

Иногда на практике более удобна следующая теорема, вытекающая из первой:

Теорема 2. Если существует предел (в предположении, что в_n0)

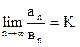(0К+),

то из сходимости ряда (В), при K<+, вытекает сходимость ряда (А), а из расходимости первого ряда, при K>0, вытекает расходимость второго. (Таким образом, при 0<К<+ оба ряда сходятся или оба расходятся одновременно).

Доказательство. Пусть ряд (В) сходится и К<+. Взяв произвольное число 0, по самому определению предела, для достаточно больших n будем иметь

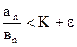, откуда а_n<(K+ )в_n.

В силу 3^о одновременно с рядом (В) будет сходится и ряд (К+)в_n, полученный умножением его членов на постоянное число К+. Отсюда, по предыдущей теореме, вытекает сходимость ряда (А).

Если же ряд (В) расходится и К>0, то в этом случае обратное отношение 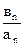имеет конечный предел; ряд (А) должен быть расходящимся, ибо если бы он сходился, то, по доказанному, сходился бы и ряд (В).

Примеры.

Исследовать сходимость ряда

.

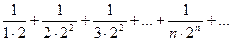Члены ряда не превосходят соответствующих членов сходящегося ряда, составленного из членов геометрической прогрессии с общим членом :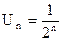

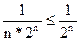(n=1,2,3,...).

Согласно теореме 1 данный ряд также сходится.

Ряд 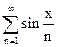(0<x<) расходится по теореме 2; в силу того, что 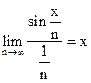и

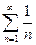расходится.

Трудность применения на практике признаков (теорем 1 и 2) сравнения состоит в необходимости иметь “запас” рядов, сходимость (или расходимость) которых известна.