Основные теоремы

Если в ряде (2) отбросить первые m членов, то получится ряд:

U_m₊₁+U_m₊₂+...+U_m₊_k+...= 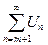, (3)

называемый остатком ряда (2) после m-ого члена.

1^о. Если сходится ряд (2), то сходится и любой из его остатаков (3); обратно, из сходимости остатка (3) вытекает сходимость исходного ряда (2).

Доказательство. Фиксируем m и обозначим k-ю частичную сумму ряда (3) через S^|_k

S^|_k=U_m₊₁+U_m₊₂+...+U_m₊_k_.

Тогда, очевидно,

S^|_k= S_m+k- S_m (4).

Если ряд (2) сходится, так что S_nS, то при неограниченном возрастании n -существует конечный предел

S^|= S - S_m (5)

и для суммы S^|_k, что и означает сходимость ряда (3). Обратно, если дано, что сходится ряд (3), так что S^|_kS^|, то перепишем равенство (4), полагая в нем R=n-m (при n>m), так:

S_n=S_m+S^|_n_-_m_.

Отсюда можно усмотреть, что при неограниченном возрастании n - частичная сумма S_n имеет предел

S=S_m+S^| (6),

т.е. сходится ряд (2).

Иными словами, отбрасывание конечного числа начальных членов ряда или присоединение вначале его нескольких новых членов не отражается на сходимости ряда.

Сумму ряда (3), если он сходится, обозначим вместо S^| символом _m, указывая значком, после какого члена берется остаток. Тогда формулы (6) и (5) перепишутся следующим образом:

S=S_m+_m, _m=S-S_m.

Если увеличивать m до бесконечности, то S_mS, а _m0. Итак:

2^о. Если ряд (2) сходится, то сумма _m его остатка после m-ого члена с возрастанием m стремится к нулю.

Упомянем следующие простые свойства сходящихся рядов:

3^о. Если члены сходящегося ряда (2) умножить на один и тот же множитель с, то его сходимость не нарушится (а сумма лишь умножится на с).

В самом деле, частичная сумм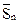а ряда

cU₁+cU₂+...+cU_n+...,

очевидно, равна

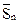= cU₁+cU₂+...+cU_n=c(U₁+U₂+...+U_n+=cS_n

и имеет пределом cА.

4^о. Два сходящихся ряда

А=а₁+а₂+...+a_n+... и

В=в₁+в₂+...+в_n+...

можно почленно складывать (или вычитать), так что ряд

(а₁в₁)+(а₂в₂)+...+(a_nв_n)+...

также сходится, и его сумма равна, соответственно, АВ.

Доказательство. Если А_n, В_n и С_n означают частичные суммы упомянутых рядов, то, очевидно

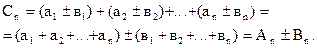
Переходя к пределу, найдем, что 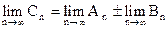, что и доказывает наше утверждение.

В заключение сделаем еще одно замечание.

5^o. Общий член U_n сходящегося ряда стремится к нулю. Это может быть доказано совершенно элементарно: S_n (а с ним и S_n-1)имеет конечный предел S, то

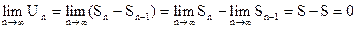Следствие. Если предел общего члена ряда при n не равен нулю, то ряд расходится.

Доказательство проведем отпротивного, т.е. допустим, что ряд сходится. Тогда в силу необходимого признака сходимости должно выполняться условие 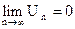. Но по условию предел общего члена ряда не равен нулю. Это противоречие означает, что предположение о сходимости ряда ошибочно; следовательно, ряд расходится.

Пример. Исследовать сходимость ряда

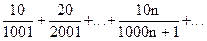Найдем предел общего члена ряда при n.

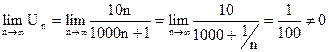Значит, данный ряд расходится.

Однако важно подчеркнуть, что необходиме условие сходимости ряда не является само по себе достаточным для сходимости ряда. Иными словами, даже при выполнении его ряд может расходится. Примером такого ряда служит ряд

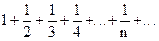который называется гармоническим. Последовательность его частичных сумм S₁=1, 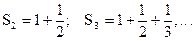монотонно возрастает, поскольку члены ряда положительны. Покажем, что она возрастает неограниченно. Для этого члены гармонического ряда, начиная с третьего, объединим в группы:

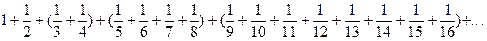В первую включим два члена (3-й и 4-й), во вторую 2²=4 члена (с 5-го по 8-й), в третью 2³=8 членов (с 9-го по 16-й) и т.д., каждый раз увеличивая вдвое число членов в группе. Таких групп, очевидно, бесконечное множество. Если заменить члены ряда в каждой группе их последними членами, то сумма членов этой группы уменьшится, т.е. справедливы неравенства

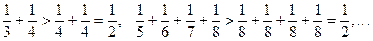
Таким образом, сумма членов каждой группы больше 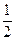, а сумма членов, включенных в достаточно большое число групп, как угодно велика. Следовательно, последовательность частичных сумм гармонического ряда неограниченно возрастает, а ряд расходится, хотя его общий член 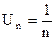при n стремится к нулю.