Доказательство. Составим частичную сумму Sn = a0 + a1 + a2 +

Составим частичную сумму S_n = a₀ + a₁ + a₂ +... + a_n.

Поскольку a_i = f(i)  1, то

S_n = f(0)1 + f(1)1 + f(2)1 +... + f(n)1

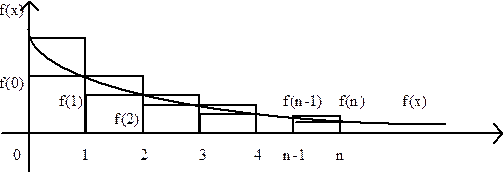
Рис. 1

Каждое слагаемое частичной суммы есть площадь прямоугольника с основанием единица и высотой, равной f(i) (Рис. 1). Добавление к частичной сумме нового члена ряда означает добавление новой площади, а потому S_n  S_n+1, то есть последовательность частичных сумм неубывающая.

Рассмотрим частичную сумму S_n-1 = a₀ + a₁ +... + a_n-1 и примем за a_i площадь прямоугольника, лежащего справа от f(i), т. е. с большей высотой. Тогда получим сумму площадей прямоугольников, часть которых расположена над кривой f(x). Эта площадь равна S_n-a_n. Рассмотрим сумму

а₁ + а₂ +... + а_n = S_n - a₀.

Каждое слагаемое этой суммы есть площадь прямоугольника с основанием, равным единице, и маленькой высотой. Тогда сумма а₁ + а₂ +... + а_n = S_n - a₀ есть сумма площадей прямоугольников, лежащих под кривой f(x). Рассмотрим

.

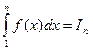С геометрической точки зрения этот интеграл есть площадь фигуры, ограниченная кривой f(x) при 0  x < n и осью Ох.

Тогда из рис. 1 имеем

S_n - a₀  J_n  S_n - a_n  S_n  J_n + a₀.

По условию теоремы существует предел

,

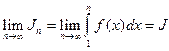тогда S_n  J+a₀. Таким образом, последовательность {S_n} ограничена сверху, а потому имеет предел, значит, ряд сходится.

Если 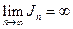, то учитывая, что S_n > J_n+a_n, откуда следует, что ряд расходится.

Доказанная теорема называется интегральным признаком Коши-Маклорена.