Распределение молекул по скоростям

В газе, находящемся в состоянии равновесия, устанав- ливается некоторое стационарное распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону.

Пусть скорости dN молекул попадают в интервал от u до u+du. Относительное число молекул, скорости которых лежат в указанном интервале, отнесённое к ширине интервала du, называется функцией распределения молекул по скоростям

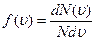. (2.9)

Функция распределения молекул газа по скоростям была получена Максвеллом и имеет следующий вид:

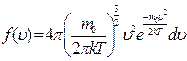. (2.10)

Здесь m₀ - масса отдельной молекулы, k – постоянная Больцмана, T – температура. Тогда число молекул, скорости которых заключены в пределах от u до u+du, определяется выражением

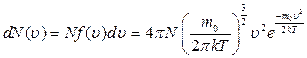, (2.11)

где N – общее число молекул.

График функции 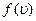представлен на рис. 2.1.

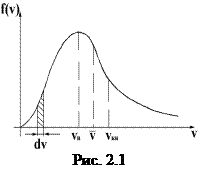
Площадь заштрихованного участка 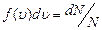равна доле молекул, скорости которых лежат в интервале от u до u+du. Просуммировав доли молекул, во всем интервале скоростей, получим единицу. Это означает, что площадь, ограниченная функцией 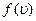и осью абсцисс, равна единице

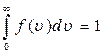. (2.12)

Выражение (2.12) представляет собой условие нормировки функции распределения молекул по скоростям.

Конкретный вид функции зависит от рода газа и от температуры. С повышением температуры максимум функции смещается вправо (рис.2.2). Площадь же, ограниченная кривой, остается неизменной, поэтому с повышением темпера- туры кривая растягивается и понижается.

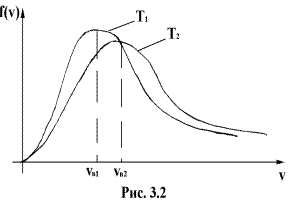
С ростом температуры увеличивается доля молекул, имеющих большую скорость. Скорость, при которой функция 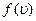достигает максимума, называется наиболее вероятнойскоростью. Этой и близкой к ней скоростью обладает наибольшее число молекул. Значение наиболее вероятной скорости можно найти из условия .

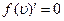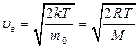, (2.13)

где m₀ - масса молекулы, М - молярная масса.

Наряду с наиболее вероятной скоростью в молекуляр- но - кинетической теории пользуются понятием средней арифметической и средней квадратичной скорости:

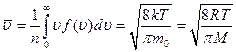, (2.14)

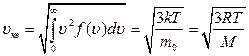. (2.15)

Значение средней квадратичной скорости, рассчитан- ной по закону Максвелла, совпадает с ранее полученным выражением (2.8).