Решение игры без седловой точки

Пусть смешанные стратегии игроков А и В заданы векторами

S_A=(p₁,p₂,….p_m) и S_B=(q₁,q_2,…….q_n), где p_i – вероятность (частота) применения игроком А чистой стратегии А_i, q_j – вероятность (частота) применения игроком В чистой стратегии B_j. Т.к. речь идет о вероятностях, то справедливо равенство

.

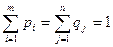Преобразование платежной матрицы

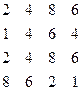
Рассмотрим игру без седловой точки

Р= .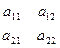

Оптимальное решение существует и определяется парой смешанных стратегий S_A =(p₁, p₂) и S_B = (q_1, q₂).

S_A = 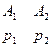, S_B =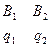

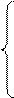
a₁₁p₁+a₂₁p₂ = V

a₁₂p₁ +a₂₂p₂ =V

р₁+р₂=1

р₁ =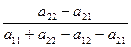

р₂ =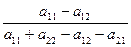

V = .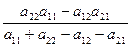

Аналогично, при отыскании смешанной стратегии второго игрока,

a₁₁q₁+a₁₂q₂ = V

a₂₁q₁ +a₂₂q₂ = V

q₁+q₂ =1

Тогда оптимальная стратегия второго игрока определяется по формулам:

q₁=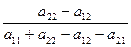

q₂=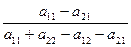

При решении любой игры рекомендуется:

1). Исключить заведомо невыгодные стратегии по сравнению с другими.

2). Определить верхнюю и нижнюю цены игры и проверить есть ли седловая точка. Если седловая точка есть, то соответствующие ей стратегии будут оптимальными и цена совпадает с нижней (верхней) игрой.

3). Если седловая точка отсутствует, то решение ищут в смешанных стратегиях.