Игры с природой

1. Критерий Лапласа опирается на принцип недостаточного ос­нования, согласно которому все состояния природы Si (i=1, 2..n) по­лагаются равновероятными. Таким образом, каждому состоянию Si соответствует вероятность qi определяемая по формуле

q_i= 1/n

Для принятия решения для каждого действия Rj вычисляется среднее арифметическое значение потерь:

M_j(R) =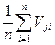

V_ji – элементы платежной матрицы.

Среди Mj(R) выбирают минимальное значение, если матрица возможных результатов представле­на матрицей потерь (или максимальное, во всех других ситуациях), которое и будет соответствовать оптимальной стратегии:

W = min{Mj(R)}

Где W - значение параметра, соответствующее оптимальной стра­тегии.

2. Критерий Вальде. Рекомендуется применять максиминную стратегию:

max min a_ij

3. Критерий максимума. Он выбирается из условия

maxmaxa_ij

4.Критерий Гурвица. Критерий рекомендует стратегию, определяемую по формуле

max(α min a_ij + (1- α)max a_ij), где α – степень оптимизма, которая изменяется в диапазоне (0, 1).

5. Критерий Сэвиджа. Суть критерия состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии.

Элемент матрицы рисков (r_ij) находится по формуле

r_ij = max a_ij – a_ij, где max a_ij – максимальный элемент в столбце исходной матрицы.

Оптимальная стратегия находится из выражения

min(max(max a_ij – a_ij)).