Задания для самостоятельной работы. 1. Дана действительная квадратная матрица порядка n

1. Дана действительная квадратная матрица порядка n.

а) Найти сумму элементов первого столбца.

б) Найти сумму элементов главной и побочной диагоналей.

2. Даны действительные числа s, t, и действительный массив a[12]. Получить:

p(1)-p(t)+(p(s-t))²-(p(1))³, где

p(x)=a[12]*x¹²+a[11]*x¹¹+...+ a[0].

3. Даны целое n, действительные массивы а[n], b[m]. В массиве а и в массиве b все элементы, следующие за элементом с наибольшим значением, заменить на 0.5.

4. Даны массивы целых чисел а[n], b[m], и целое k. Если в массиве а нет ни одного элемента со значением k, то первый по порядку элемент этого массива, не меньший всех остальных элементов, заменить на значение k. По такому же правилу преобразовать массив b применительно к значению 10.

5. Даны действительные числа s, t. Получить:

f(t,-2*s,1.17)+f(2.2,t,s-t),

2*a-b-sin(c)

где f(a,b,c)= ───────

5+abs(c)

6. Даны действительные числа s, t. Получить:

g(1.2,s)+g(t,s)-g(2*s-1,s*t),

a² + b²

где g(a,b)= ───────────

a² +2*a*b+3*b² +4

7. Даны действительные числа x, y, z. Получить:

h(1,2,3)+h(x,y,z),

max(a,a+b)+max(a,b+c)

где h(a,b,c)= ──────────────.

1+max(a+b*c,1.15)

8. Даны действительные числа a, b. Получить:

u=min(a,b), v=min(a*b,a+b), min(u+v²,(u+v)+3.14).

9. Даны действительные числа n, m, целые массивы а[n], b[m], c[30]. Получить:

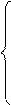min(b(0),...,b(m))+min(c(0),...,c(30))

T = при abs(min(a(0),...,a(n))) > 10,

1+(max(c(0),...,c(30))) в противном случае.

10. Даны натуральные числа k, l, m, действительные массивы х[k], y[l], z[m]. Получить:

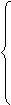(max(y(0),...,y(l))+max(z(0),...,z(m)))/2

t= при max(x(0),...,x(k)) >=0,

(max(x(0),...,x(k)))² в противном случае.

11. Дано натуральное число n. Среди чисел 1,2,...,n найти все те, которые можно представить в виде суммы квадратов двух натуральных чисел. (Определить метод, позволяющий распознать полные квадраты).

12. Даны действительные числа x(0), y(0), x(1), y(1),...,x(10), y(10). Найти периметр многоугольника, вершины которого имеют соответственно координаты (x(0), y(0)), (x(1), y(1)),...,(x(10), y(10)). (Определить метод вычисления расстояния между двумя точками, заданными своими координатами.)

13. Даны натуральное число n, действительные числа x(0), y(0), x(1), y(1),...,x(n), y(n). Найти площадь многоугольника, вершины которого при некотором последовательном обходе имеют координаты (x(0), y(0)), (x(1), y(1)),...,(x(n), y(n)). (Определить метод вычисления площади треугольника по координатам его вершин.)

14. Дано натуральное число n. Выяснить, имеются ли среди чисел:

n, n+1,...,2*n - близнецы, т.е. простые числа, разность между которыми равна двум. (Определить метод, позволяющий распознавать простые числа.)

15. Определить полусумму длин двух векторов А[3], В[5]. Длина вектора определяется как корень квадратный из суммы квадратов его проекций. (Использовать метод определения длины вектора).

16. Найти среднее геометрическое положительных элементов каждого столбца матрицы А[10,15].

17. Даны две матрицы А[5,5] и В[6,6]. Определить полусумму следов матриц.

18. Определить метод нахождения корней нелинейных уравнений вида f(x)=0 методом половинного деления, a*x⁴+b*x²+c*x+d=0, где a,b,c - массивы из трех чисел, d-const.

19. Определить метод вычисления чисел Мaрсена из интервала (1, n), n - задано. (Простое число называется числом Мaрсена, если оно может быть представлено в виде 2^p-1, где р - тоже простое число.)

20. Заданы вещественные массивы А[10], В[8]. Определить метод, заменяющий в заданном массиве все отрицательные элементы на нули.

21. Даны действительные числа s,t. Получить:

f(t,- 2*s, 1.17)+f(2.2,t,s-t),

где

2*a-b-sin(c)

f(a,b,c) = ───────────.

5 + abs(c)

22. Даны действительные числа s,t. Получить:

g(1.2, s)+g(t, s)-g(2s-1,st),

где

a²+b²

g(a,b) = ──────────────

a²+2*a*b+3*b²+4

23. Дано действительное число y. Получить:

1.7*t(0.25)+2*t(1+y)

──────────────,

6-t(y²-1)

4 x+1

S ────

k=0 (2*k+1)!

где t(x) = ──────────

4 x*k

S ────

k=0 (2*k)!

24. Даны действительные числа a, b, c. Определить метод, вычисляющий

max(a,a+b)+max(a,b+c)

───────────────

1+max(a+b*c,1+a,15)

25. Даны действительные числа a, b. Получить:

u=min(a,b), v=min(a*b,a+b)*min(u+a², 3.14).

26. Даны две квадратные матрицы порядка 5. Найти последовательность из нулей и единиц b такую, что b[i]=1, когда все элементы i-й строки первой матрицы содержатся в i-й строке второй матрицы.

27. Дана действительная квадратная матрица порядка n. Найти наибольшее из значений элементов первой и последней строк.

28. Даны действительные числа s,t. Получить:

h(s,t)+max(h(s-t,s*t), h(s-t,s+t) ²)+ h(1,1),

где

a b

h(a, b) = ────── + ─────── - (a-b)³.

1+b² 1+a²

29. Дан действительный массив a[6]. Получить для x=1,3,4 значения p(x+1)-p(x), где

p(y)=a[6]*y⁶ + a[5]*y⁵ +... + a[0].

30. Даны действительные числа s, t и действительный массив a[8]. Получить:

p(1)-p(t)+p(s-t)-p(1), где

p(x)=a[8]*x⁸ + a[7]*x⁷ +... + a[0].

31. Даны действительные массивы a[n], b[m]. В массиве a и в массиве b все элементы, следующие за элементом с наибольшим значением (за первым по порядку, если их несколько), заменить на 0.5.

32. Даны целые массивы a[n], b[m] и целое k. Если в массиве a нет ни одного элемента со значением k, то первый по порядку элемент этой последовательности, не меньший всех остальных элементов, заменить на значение k. По такому же правилу преобразовать массив b применительно к значению 11.

33. Даны целые числа a, b и массивы целых чисел n[7], d[7].

Вычислить по схеме Горнера

n[7] * a⁷ + n[6] * a⁶ +... + n[0]

───────────────────

d[7] * b⁷ + d[6] * b⁶ +... + d[0]

определив метод полного сокращения рационального числа, заданного числителем и знаменателем, а также методы сложения и умножения рациональных чисел.

Схема Горнера (для n=3):

a[3]*x³ + a[2]*x² + a[1]*x + a[0] = (a[3]*x² + a[2]*x + a[1])*x + a[0] =

((a[3]*x +a[2])*x + a[1])*x + a[0]

34. Даны натуральное число n, действительные числа x, y и массивы действительных чисел a[n], b[n]. Вычислить по схеме Горнера (см. задание 33) значение многочлена с комплексными коэффициентами:

(a[n]+i*b[n])(x+i*y)n + (a[n]-1+i*b[n]-1)(x+i*y)(n-1)+...+ (a[0]+i*b[0]).

(Определить методы выполнения арифметических операций над комплексными числами).

35. Даны натуральное число n, массив целых чисел a[n]. Рассмотреть отрезки последовательности a[n] (подпоследовательности идущих подряд членов), состоящие из:

а) полных квадратов;

б) степеней пятерки.

В каждом случае получить наибольшую из длин рассматриваемых отрезков. (Определить методы, позволяющие распознавать полные квадраты, степени пятерки, простые числа).

36. Даны натуральное число n, массив целых чисел a[n]. Рассмотреть отрезки последовательности a[n] (подпоследовательности идущих подряд членов), состоящие из простых чисел. Получить наибольшую из длин рассматриваемых отрезков. (Определить метод, позволяющий распознавать простые числа).

37. Даны натуральное число n, массив целых чисел a[n]. Рассмотреть все отрезки последовательности a[n] (см. задачу 35), состоящие из совершенных чисел. (Определить метод, позволяющий распознавать совершенные числа).

38. Дана действительная квадратная матрица порядка n. Найти наименьшее из значений элементов побочной диагонали и двух соседних с ней линий.

39. Дана действительная квадратная матрица порядка n. Для данного натурального m (m<=2*n) найти сумму тех элементов матрицы, сумма индексов которых равна m.

40. Выяснить: верно ли, что наибольшее из значений элементов главной диагонали действительной квадратной матрицы порядка n больше, чем наименьшее из значений элементов побочной диагонали.

41. Даны массивы действительных чисел x[5], y[5]. Точки с координатами (x[0], y[0]), (x[1], y[1]), (x[2], y[2]) рассматриваются как вершины первого треугольника, точки с координатами (x[3], y[3]), (x[4], y[4]), (x[5], y[5]) - второго треугольника. Выяснить, верно ли, что первый треугольник целиком содержится во втором. (Определить метод, позволяющий выяснить, лежат ли две точки в одной полуплоскости относительно заданной прямой и метод вычисления расстояния между двумя точками).

42. Два треугольника заданы координатами своих вершин так, что один треугольник целиком содержится во втором. Определить площадь области, принадлежащей внешнему треугольнику, но не принадлежащей внутреннему треугольнику. (Определить метод, позволяющий выяснить, лежат ли две точки в одной полуплоскости относительно заданной прямой, а также метод вычисления площади треугольника по трем сторонам).

43. Даны массивы натуральных чисел x[3], y[3]. Точки с координатами (x[0], y[0]), (x[1], y[1) рассматриваются как диагональные вершины первого прямоугольника, точки с координатами (x[2], y[2]), (x[3], y[3]) – второго, лежащего внутри первого. Провести вычисления, аналогичные тем, которые были описаны в предыдущей задаче в отношении треугольников. Стороны прямоугольников считаются параллельными осям экрана.

44. Даны две целочисленные квадратные матрицы порядка 6. Найти последовательность из нулей и единиц b[6] такую, что b[i]=1, когда все элементы i-й строки первой матрицы больше соответствующих элементов i-й строки второй матрицы.

45. Даны две целочисленные квадратные матрицы порядка 6. Найти последовательность из нулей и единиц b[6] такую, что b[i]=1, когда все элементы i-х строк первой и второй матриц отрицательны.

46. Даны две целочисленные квадратные матрицы порядка 5. Найти последовательность из нулей и единиц b[5] такую, что b[i]=1, когда i-е строки первой и второй матриц содержат вместе не более трех положительных элементов.

47. Даны две целочисленные квадратные матрицы порядка 6. Найти последовательность из нулей и единиц b[6] такую, что b[i]=1, когда количество отрицательных и неотрицательных элементов i-й строки первой матрицы совпадает соответственно с количеством отрицательных и неотрицательных элементов i-й строки второй матрицы.

48. Два треугольника заданы координатами своих вершин так, как указано в задаче 41. Определить, какой треугольник имеет больший периметр.

49. Даны действительные числа s,t. Получить f(t,s²,3.56)+f(2.4,t,abs(s-t)),

где

2*cos(a)-b-sin(c)

f(a,b,c) = ───────────.

5+abs(a)+abs(b)

50. Даны действительные числа s,t. Получить g(7,s-t)+g(7,s+t)-g(s-1,s*t),

где ┌───

\| a²+b²

g(a,b) = ──────.

a²+b²

51. Даны действительные числа a, b, c. Получить функцию, вычисляющую:

min(a,c)+max(a,b)+sign(a)

────────────────.

1+max(a+b*c,15)

Математическая функция sign(x) даёт (-1) при x<0, 0 при x=0, и 1 при x>0.

52. Дано действительное число y.

Получить:

1.3*t(y)-2*t(1+y)

─────────,

6-t(y²-1)

7 x+1

Õ ─────

k=0 (2*k+1)!

где t(x) = ───────────

8 x*k

Õ ─────

k=1 (2*k)!

53. Даны действительные числа a,b. Получить:

u(a,b²)-v(b,a²)

где

u(x,y)=sin(x)*min(x,y),

v=min(x*y,x+y)*min(y+x²,6.2832).

54. Даны натуральные числа k, l, m, массивы действительных чисел x[k], y[l], z[m]. Получить:

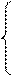(min(y[1..l])+max(z[1..m]))/2

F= при min(x[1],...,x[k])>0,

(max(x[1],..., x[k]))³ в противном случае.

55. Дан массив действительных чисел a[6]. Получить для x=2 значения f(x²)+f(x³), где f(y)=a[0]*y⁶ + a[1]*y⁵ +... + a[6].

56. Даны действительные числа d,t и массив действительных чисел a[7]. Получить:

p(15)-p(t-5)+p(d+t)-p(1), где

p(y)=a[7]*y⁷ + a[6]*y⁶ +... + a[0].

57. Даны натуральные числа n, m и массивы действительных чисел a[n], b[m]. В массиве a и в массиве b все элементы, перед элементом с наименьшим значением модуля (за первым по порядку, если их несколько), заменить на противоположные.

58. Даны две квадратные матрицы порядка 5. Найти последовательность из нулей и единиц b[5] такую, что b[i]=1, когда 2 элемента i-й строки первой матрицы больше соответствующих элементов i-го столбца второй матрицы.