Для решения таких уравнений используется функция odesolve(x,b,[step]), где x – переменная интегрирования, b – верхняя граница интервала интегрирования, необязательный параметр step – количество шагов, используемых решателем при поиске решения. Чем выше величина step, тем точнее решение, но тем больше времени потребуется на его поиск.
При использовании функции odesolve само уравнение, а также его начальные условия задаются в блоке решения уравнений, который начинается со слова given. Начальные условия можно записывать только в виде равенств, их количество должно равняться степени уравнения. В случае, если для решения уравнения используются не начальные, а граничные условия, их следует записывать также в виде равенств и определять в точке, соответствующей аргументу b. Следует помнить, что начальные или граничные условия вида 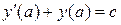 не поддерживаются Mathcad.
не поддерживаются Mathcad.
Пример решения дифференциального уравнения указанным методом (в указанном примере будет возвращена функция F(t), в дальнейшем можно построить ее график и график ее производной):
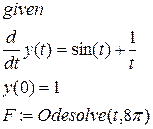
Функция может решать уравнение одним из трех численных методов. Для переключения между ними следует воспользоваться контекстным меню при щелчке правой кнопкой мыши по названию функции.
Системы обыкновенных дифференциальных уравнений первого порядка, линейных относительно производной
Функция odesolve(vector,x,b,[step]) также может использоваться для решения систем обыкновенных дифференциальных уравнений первого порядка. В этом случае у функции появляется дополнительный аргумент vector, представляющий собой вектор, состоящий из названий функций, входящих в систему.(без скобок с указанием аргументов). В результате своей работы функций возвратит вектор, состоящий из функций от переменной интегрирования, причем именно аргумент vector задает порядок следования функций. В остальном использование функции аналогично случаю решения одиночного дифференциального уравнения. Пример (в результате будут созданы функции F(t), G(t) и H(t)):
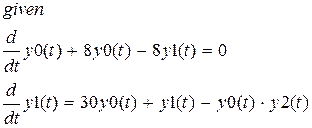
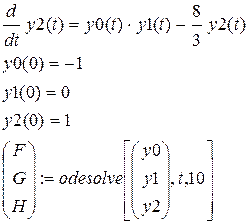
Обыкновенные дифференциальные уравнения, нелинейные относительно высшей производной, и системы обыкновенных дифференциальных уравнений первого порядка, нелинейных относительно производной
Для решения таких уравнений в Mathcad используется ряд специальных функций, каждая из которых реализует свой численный метод дифференцирования: rkfixed (метод Рунге-Кутты с фиксированным шагом интегрирования), Rkadapt (метод Рунге-Кутты с автоматически изменяющимся шагом интегрирования), Bulstoer (метод Булирша-Штоера), Stiffb (также метод Булирша-Штоера для решения жестких систем уравнений, дополнительно требуется матрица Якоби системы исходных уравнений), Stiffr (метод Розенброка для решения жестких систем уравнений, дополнительно требуется матрица Якоби системы исходных уравнений), Radau (метод RADAU5 для решения жестких систем уравнений, матрица Якоби не требуется). Жесткими уравнениями принято считать такие, для которых классические методы не в состоянии найти решение, или это решение оказывается неустойчивым либо неточным. Следует обратить внимание, что все функции, кроме rkfixed, пишутся с заглавной буквы (т.к. имеют место аналогичные функции с малой буквы, с другим синтаксисом и другими задачами). Синтаксис этих функций рассмотрим на примере функции rkfixed.
Для решения системы уравнений с использованием данных функций не используется блок решения уравнений. Вместо этого функция работает с матричным представлением системы дифференциальных уравнений. Для приведения системы уравнений к данному виду следует выполнить следующие действия:
1. Записать систему таким образом, чтобы у каждого уравнений была левая и правая часть. Левая часть каждого уравнения должна представлять собой производную соответствующей функции. Коэффициенты и иные алгебраические выражения при данной производной недопустимы;
2. Задаются именем вектора, элементы которого будет представлять собой функции, присутствующие в системе дифференциальных уравнений. В рассмотренном ниже примере функция y0(t) будет соответствовать первому элементу вектора Y (Y0). На этом же этапе определяются с порядком следования функций в векторе имен. Однако ничего присваивать элементам вектора не нужно;
3. Определяют пользовательскую вектор-функцию, аргументами которой является имя переменной интегрирования и имя вектора (см. пункт 2, порядок важен!). Количество элементов вектор-функции равно количеству уравнений в системе. Каждому элементу вектор-функции присваивают правую часть соответствующего уравнения системы, в котором имена функций (с аргументами в скобках) заменяют на элементы вектора из пункта 2. Такое преобразование называется приведением системы уравнений к стандартному виду Mathcad;
4. Определяют вектор начальных условий, каждый элемент которого равен значению соответствующей функции в некой начальной точке;
5. Для функций Stiffb и Stiffr путем тождественных преобразований (вручную или с помощью символьных операций Mathcad, см. следующую лабораторную работу) составляют матрицу Якоби системы уравнений;
6. Используя функцию rkfixed или аналогичную, решают систему уравнений. Синтаксис функции: rkfixed(Y,x1,x2,npoints,D) (Stiffb(Y,x1,x2,npoints,
D,J)), где Y – имя вектора начальных условий, см. пункт 4; x1 и x2 – границы интервала интегрирования; npoints – количество точек, в которых ищется значение, высокие значения могут существенно замедлить поиск решения; D – вектор-функция правых частей уравнения, см. пункт 3; J – матрица Якоби;
7. Результатом работы функции является матрица, первый столбец которой содержит значения переменной интегрирования, а каждый последующий – значение соответствующей функции (в том порядке, который был определен в пункте 2). Количество строк матрицы равно величине npoints.
В дальнейшем найденные решения можно отобразить на графике, в частности, построив графики второго и последующего столбцов результирующей матрицы относительно ее первого столбца.
Пример решения рассмотренной выше системы уравнения с использованием функции Rkadapt:
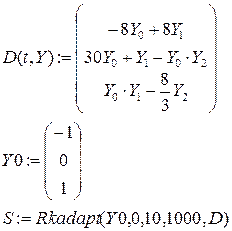
Функции могут также использоваться для решения одиночных уравнений, в этом случае аргументы Y и D будут не векторами, а скалярными величинами.
 2015-05-14
2015-05-14 744
744








