Задание к лабораторной работе

Построим с помощью элементов библиотеки Enterprise Library модель простой системы массового обслуживания – модель банковского отделения.

В банковском отделении находятся банкомат и стойки банковских кассиров, которые предназначены для быстрого обслуживания посетителей банка. Операции с наличностью клиенты банка производят с помощью банкомата, а более сложные операции, такие как оплата счетов, – с помощью кассиров.

1. Создайте новую модель. В свойствах эксперимента Simulation задайте выполнение модели в режиме реального времени с выполнением одной единицы модельного времени в одну секунду. В этой модели под единицей модельного времени мы будем понимать одну минуту работы банковского отделения.

2. Создайте блок-схему модели, которая пока будет состоять только из банкомата. Для этого перетащите в окно структуры элементы библиотеки Enterprise Library и соедините их так, как показано на рис. 4.

Объект source генерирует заявки (entities) определенного типа через заданный временной интервал. Заявки представляют собой объекты, которые производятся, обрабатываются, обслуживаются или еще каким-нибудь образом подвергаются воздействию моделируемого процесса: это могут быть клиенты в системе обслуживания, детали в модели производства, документы в модели документооборота и др. В нашем примере заявками будут посетители банка, а объект source будет моделировать их приход в банковское отделение.

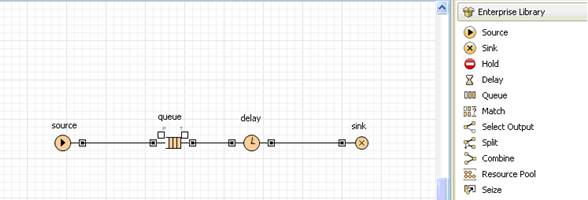
Рис. 4.

Объект queue моделирует очередь клиентов, ожидающих обслуживания.

Объект delay моделирует задержку. В нашем примере он будет имитировать банкомат, тратящий определенное время на обслуживание клиента.

Объект sink обозначает конец блок-схемы.

3. Запустите модель.

Для каждой модели, созданной в Enterprise Library, автоматически создается блок-схема с наглядной визуализацией процесса, с помощью которой вы можете изучить текущее состояние модели, например, длину очереди, количество обслуженных человек и т.д.

Для запуска модели щелкните мышью по кнопке Запустить. Откроется окно с презентацией запущенного эксперимента. AnyLogic автоматически помещает на презентацию каждого простого эксперимента заголовок и кнопку, позволяющую запустить модель и перейти на презентацию (рис. 5), нарисованную вами для главного класса активного объекта этого эксперимента (Main). Щелкните по этой кнопке. AnyLogic переключится в режим работы модели. С помощью визуализированной блок-схемы проследите, сколько человек находится в очереди, сколько человек в данный момент обслуживается и т.д.

Рис. 5.

Попробуйте изменить скорость выполнения модели, переключиться в виртуальный режим. Во время выполнения модели можно следить за состоянием любого блока диаграммы процесса с помощью окна инспекта этого объекта (рис. 6). Чтобы открыть окно инспекта, щелкните мышью по значку блока. В окне инспекта будет отображена базовая информация по выделенному блоку, например, для блока Queue будет отображена вместимость очереди, количество заявок, прошедшее через каждый порт объекта, и т.д.

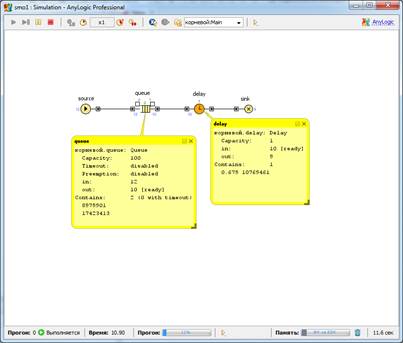
Рис. 6.

Встройте в файл отчета полученные характеристики процесса обслуживания. Сколько клиентов пришло в банк и сколько обслужилось на момент окончания прогона модели?

4. Задайте данные модели, изменяя свойства созданных объектов (рис. 7).

Откройте окно свойств объекта source, перейдите на вкладку Параметры. В свойстве interarrivalTime укажите, как часто в отделение приходят клиенты – exponential (0.67).

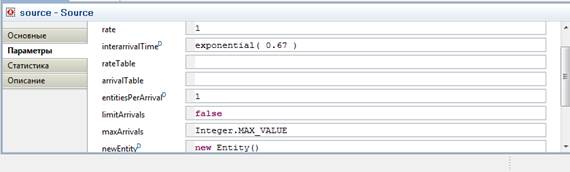
Рис. 7.

Интервал между приходом клиентов распределен экспоненциально со средним значением, равным 1.5 единицы модельного времени. Заметьте, что аргумент функции exponential () равен 0.67, потому что в качестве аргумента задается интенсивность прихода клиентов.

Функция exponential () является стандартной функцией генератора случайных чисел AnyLogic. AnyLogic предоставляет функции и других случайных распределений, таких как нормальное, равномерное, треугольное и т.д. За детальным описанием функций и их параметров обращайтесь к руководству пользователя или справочнику классов (см. методы класса Func). Для вызова руководства пользователя, справочника классов AnyLogic выберите соответствующие пункты меню Справка.

В свойстве capacity объекта queue (рис. 8) задайте максимальную длину очереди – 15.

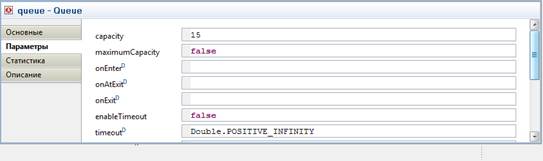
Рис. 8.

В свойстве delayTime объекта delay (рис. 9) задайте время задержки (время обслуживания) – triangular (0.8, 1, 1.3).

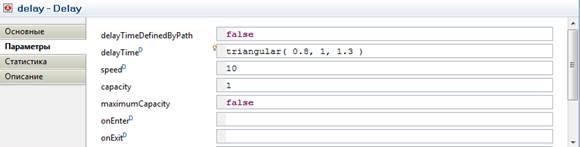
Рис. 9.

Обслуживание одного клиента занимает примерно 1 минуту. Здесь время обслуживания распределено по треугольному закону со средним значением, равным 1 минуте, минимальным – 0.8 и максимальным – 1.3 минуты.

5. Запустите модель и проанализируйте ее работу. Как изменились характеристики процесса обслуживания? Сравните результаты с предыдущим прогоном.

6. Включите сбор статистики для блоков queue и delay.

AnyLogic позволяет производить сбор сложной статистики. Для этого нужно лишь включить у объекта режим сбора статистики, поскольку по умолчанию он отключен для повышения скорости выполнения модели.

В системе собирается статистика по длине очереди для блока queue (length) и статистика по коэффициенту использования для блока delay (utilization). Чтобы включить сбор статистики для объекта, установите переключатель Включить сбор статистики на вкладке Основные свойств объекта.

Запустите модель и просмотрите в окне инспекта статистику для блоков queue и delay. Каковы средняя длина очереди посетителей к банкомату и загрузка банкомата?

7. Добавьте в модель банковских кассиров.

Можно моделировать число кассиров, как и банкомат, с помощью объектов delay. Но удобнее моделировать число кассиров с помощью ресурсов (многоканальное устройство). Ресурс – это специальный объект Enterprise Library, который может потребоваться заявке для выполнения какой-то задачи. В нашем примере посетителям банковского отделения (заявкам) необходимо получить помощь у банковских служащих (ресурсов).

Добавьте на диаграмму следующие объекты:

1) selectOutput – является блоком принятия решения. В зависимости от заданного вами условия, заявка, поступившая в этот объект, будет поступать на один из двух выходов объекта. Оставьте все свойства объекта без изменений. Пусть выход true выбирается С заданной вероятностью, а Вероятность [0..1] равна 0.5. В этом случае к кассирам и банкомату будет приходить примерно равное количество клиентов;

2) service – блок захватывает для заявки заданное количество ресурсов, задерживает заявку, а затем освобождает захваченные ею ресурсы. В нашей модели этот объект будет моделировать обслуживание клиента кассиром (или каким-то другим служащим банковского отделения). Задайте следующие свойства объекта: укажите, что в очереди к кассирам может находиться до 20 человек (свойство queueCapacity); задайте время обслуживания (свойство delayTime). Будем полагать, что время обслуживания имеет треугольное распределение с минимальным средним значением 2.5, средним – 6 и максимальным – 11 минут;

3) ResourcePool – задает ресурсы определенного типа. Он должен быть подсоединен к объектам, моделирующим занятие и освобождение ресурсов (в нашем случае это объект Service). В нашем случае моделирует банковских кассиров. Перейдите в окно свойств объекта и задайте число кассиров (свойство capacity) – 4.

Соедините объекты соответствующим образом (рис. 10).

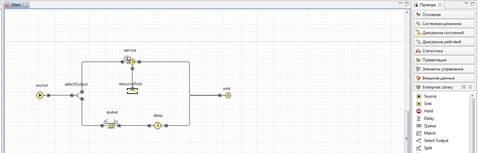
Рис. 10.

8. Запустите модель. Сколько посетителей обслужилось у банковских работников и сколько у банкомата? Какова средняя длина очереди к банкомату? Оцените занятость кассиров и банкомата.

9. Создайте анимацию модели.

Сначала изобразим на анимации следующие элементы: банкомат (в виде кружка) и ведущую к нему очередь клиентов (в виде ломаной); клиентов анимируем человечками; две диаграммы для отображения статистики занятости банкомата и очереди к банкомату. Анимация модели рисуется в той же диаграмме (в графическом редакторе), в которой задается и диаграмма моделируемого процесса (см. рис. 11).

1) Перетащите элемент Овал из палитры Презентация на диаграмму класса активного объекта.

2) Перейдите на страницу Динамические панели свойств данной фигуры. В поле Цвет заливки введите следующую строку: delay.size () > 0? red: green. Здесь delay – это имя нашего объекта Delay. Функция size () возвращает число человек, обслуживаемых в данный момент времени. Во время моделирования будет меняться цвет фигуры. Если банкомат занят, то цвет кружка будет красным, в противном случае – зеленым.

3) На странице свойств объекта delay введите в поле Фигура анимации имя нашего овала: oval. Выберите из выпадающего списка Тип анимации – Одиночная.

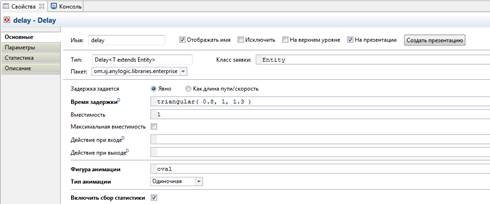
4) Нарисуйте ломаную, которая будет обозначать на анимации очередь к банкомату (см. рис. 12). Чтобы нарисовать ломаную, сделайте двойной щелчок мышью по элементу Ломаная в палитре (при этом его значок должен поменяться на этот: ). Далее рисуйте ломаную точка за точкой, последовательно щелкая мышью в тех точках диаграммы, куда Вы хотите поместить вершины ломаной. Чтобы завершить рисование, добавьте последнюю точку ломаной двойным щелчком мыши. Очень важно, какую точку ломаной Вы создаете первой. Заявки будут располагаться вдоль нарисованной Вами ломаной в направлении от конечной к начальной. Поэтому рисуйте ломаную слева направо и поместите рядом с банкоматом конечную точку ломаной, которая будет соответствовать в этом случае началу очереди.

5) На странице свойств объекта queue введите polyline в поле Фигура анимации.

6) Создайте анимацию клиента. Откройте палитру Картинки. Эта палитра содержит набор картинок, которые наиболее часто используются пользователями AnyLogic при создании моделей. Перетащите элемент Человек из палитры на диаграмму графического редактора и поместите ее за границу видимой области презентации (т.е. выше верхней границы презентации). Для этого понадобится передвинуть весь холст диаграммы немного вниз (нажмите правую кнопку мыши и перетащите мышь, не отпуская кнопки), затем поднимите холст обратно. По умолчанию эта картинка будет называться person.

7) Перейдите в окно свойств объекта source. В поле Фигура анимации заявки введите имя нашей фигурки человека: person.

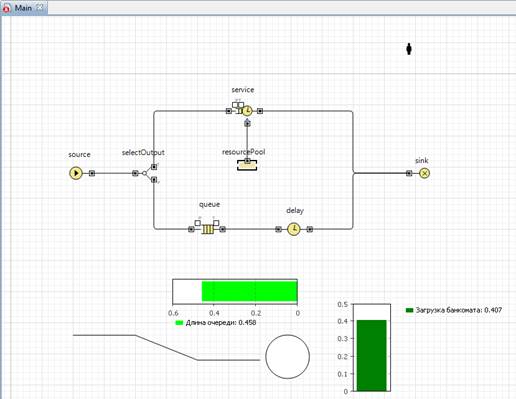
Рис. 11.

8) Перейдите в окно свойств эксперимента. На вкладке модельное время в выпадающем меню Остановить выберите – нет.

9) Запустите модель. Увеличьте скорость выполнения модели. Пронаблюдайте за анимацией Вашей модели.

10) Добавьте диаграмму для отображения средней занятости банкомата. Для этого перетащите элемент Столбиковая диаграмма из палитры Статистика на диаграмму класса и поместите ее справа от фигуры банкомата.

11) Перейдите на страницу Основные панели свойств диаграммы. Щелкните мышью по кнопке Добавить элемент данных. При этом появится секция свойств того элемента данных, который будет отображаться на этой диаграмме. Измените Заголовок на Загрузка банкомата.

12) Введите delay.statsUtilization.mean () в поле Значение. Здесь delay – это имя нашего объекта Delay. У каждого объекта Delay есть встроенный набор данных statsUtilization, занимающийся сбором статистики использования этого объекта. Функция mean () возвращает среднее из всех измеренных этим набором данных значений. Вы можете использовать и другие методы сбора статистики, такие, как min () или max (). Полный список методов можно найти на странице документации этого класса набора данных: StatisticsContinuous (на английском языке).

13) Перейдите на страницу Внешний вид панели свойств. Измените расположение легенды диаграммы (справа относительно диаграммы) с помощью кнопок Расположение. Измените размер диаграммы, как показано на рис. 11.

14) Аналогичным образом добавьте еще одну столбиковую диаграмму для отображения средней длины очереди. Измените ее размер, как показано на рис. 11. Перейдите на страницу Внешний вид панели свойств диаграммы и измените направление столбцов диаграммы так, чтобы столбцы столбиковой диаграммы росли влево.

15) Добавьте элемент данных, который будет отображаться на диаграмме. Задайте Заголовок: Длина очереди и задайте Значение: queue.statsSize.mean (). Здесь statsSize – это имя объекта типа «статистика» StatisticsContinuous, производящего сбор статистики размера очереди объекта Queue.

16) Запустите модель и пронаблюдайте за занятостью банкомата и средней длиной очереди с помощью только что созданных диаграмм.

Теперь добавим анимацию для банковских кассиров (см. рис. 12):

17) Нарисуйте ломаную, которая будет отображать очередь клиентов, ожидающих обслуживания кассирами. Рисуйте ее, как и раньше, слева направо.

18) Справа от этой ломаной нарисуйте еще одну, из четырех точек, чтобы указать на анимации места, в которых будут находиться банковские служащие.

19) Нарисуйте на презентации кассиров. Будем отображать их одной из двух картинок – одна будет показывать занятого кассира, а другая – свободного. Для этого перетащите элемент Изображение из палитры Презентация в то место диаграммы, где у нас находится человечек. Перейдите в панель Свойства. Щелкните мышью по кнопке Добавить и выберите файл изображения, которое будет отображать данная фигура. Картинка busy.png (изображение занятого клерка) находится в каталоге <каталог AnyLogic>\resources\tutorials\Bank Office. Чтобы сохранить исходный размер изображения, установите флажок Исходный размер.

20) Аналогичным образом добавьте изображение занятого кассира (клерка).

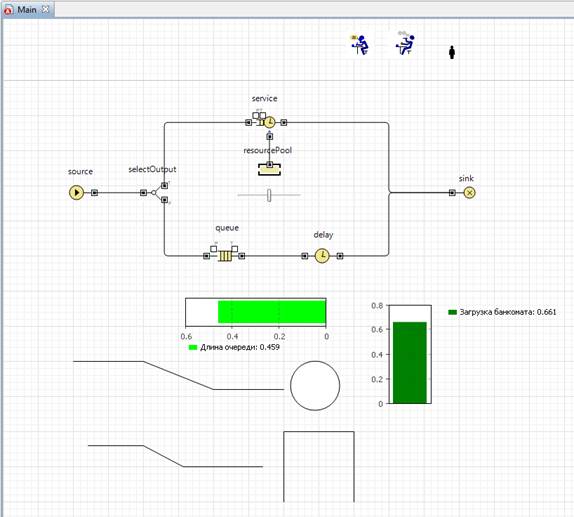
Рис. 12.

21) Перейдите в окно свойств объекта service. Введите polyline 1 (имя ломаной, задающей форму очереди, ведущей к кассирам) в поле Фигура анимации (queue).

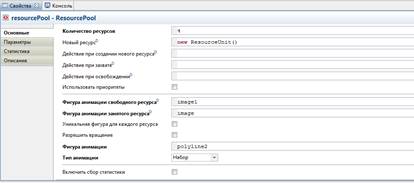
22) Перейдите в окно свойств объекта resourcePool. В поле Фигура анимации введите имя ломаной, задающей местоположение кассиров на презентации: polyline 2. Выберите Набор из выпадающего списка Тип анимации. В поле Фигура анимации свободного ресурса введите имя изображения свободного клерка: image 1. В поле Фигура анимации занятого ресурса введите image.

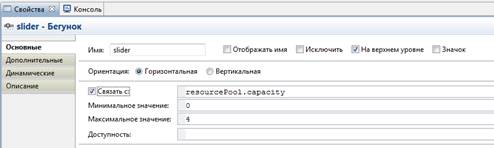
23) Откройте палитру Элементы управления и перетащите элемент Бегунок из палитры на нашу диаграмму. Поместите бегунок под объектом ResourcePool, чтобы было понятно, что с помощью этого бегунка будет меняться количество ресурсов, задаваемых именно этим объектом (см. рис. 12).

24) Перейдите в окно свойств данного элемента. Введите 4 в поле Максимальное значение (будем варьировать количество клерков от 0 до 4). Введите resourcePool.capacity в поле Связать с.

10. Запустите модель. Пронаблюдайте за созданной анимацией. Попробуйте изменить количество кассиров. Образуется ли очередь перед кассирами? Сделайте вывод о том, сколько служащих необходимо для нормальной работы банковского отделения при заданной интенсивности прихода клиентов. Как посмотреть статистику занятости каждого кассира?

11. Добавьте в модель сбор статистики о времени обслуживания клиента.

Необходимо определить, сколько времени клиент проводит в банковском отделении и сколько времени он теряет, ожидая своей очереди. Такая статистика собирается с помощью специальных объектов сбора данных. Собранная статистика распределения времени обслуживания клиентов отображается с помощью гистограмм.

1) Создайте класс сообщения Customer (сообщения этого класса будут представлять клиентов банковского отделения). Для этого в панели Проект, щелкните правой кнопкой мыши по элементу модели и выберите Создать | Java класс из контекстного меню. В диалоговом окне Новый Java класс в поле Имя введите имя нового класса Customer (рис. 13); выберите из выпадающего списка Базовый класс полное имя данного класса: com.xj.anylogic.libraries.enterprise.Entity (этот класс будет наследоваться от базового класса заявки Entity). Щелкните по кнопке Далее.

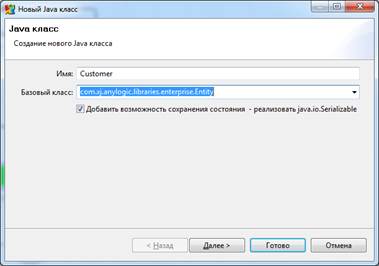
Рис. 13

2) На второй странице мастера задайте параметры создаваемого Java-класса: enteredSystem тип double для сохранения момента времени, когда клиент пришел в банковское отделение; startWaiting тип double для сохранения момента времени, когда клиент встал в очередь к банкомату (рис. 14).

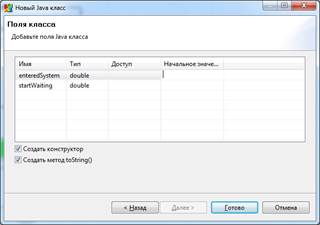
Рис. 14

3) Щелкните по кнопке Готово. Откроется редактор кода созданного класса (можно его закрыть).

Добавим элементы сбора статистики. Эти элементы будут запоминать соответствующие значения времени для каждого клиента и предоставят пользователю стандартную статистическую информацию: среднее, минимальное, максимальное из измеренных значений, среднеквадратичное отклонение, доверительный интервал для среднего и т.п.

4) Перетащите элемент Данные гистограммы с палитры Статистика на диаграмму класса Main. Задайте свойства элемента: Кол-во интервалов – 50; Нач. размер интервала – 0.01; измените Имя на waitTimeDistr.

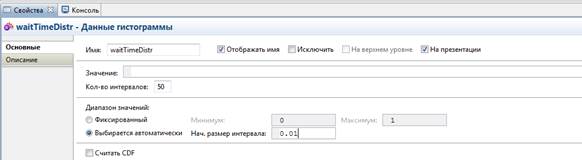
5) Создайте еще один элемент сбора данных гистограммы (Ctrl + перетащите только что созданный объект данных гистограммы, чтобы создать его копию). Измените Имя этого элемента на timeInSystemDistr.

6) Перейдите в свойства блока source и задайте новые свойства. Измените поле Класс заявки на Customer. В поле Новая заявка – введите new Customer(). Это позволит напрямую обращаться к полям класса заявки Customer в коде динамических параметров этого объекта. В поле Действие при выходе Введите entity.enteredSystem = time();. Этот код будет сохранять время создания заявки-клиента в переменной enteredSystem нашего класса заявки Customer. Функция time() возвращает текущее значение модельного времени.

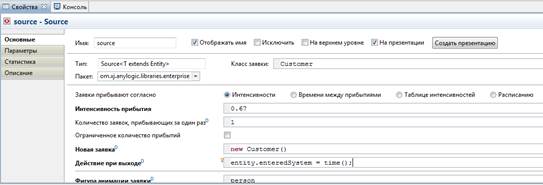
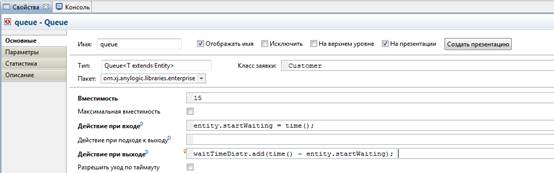
7) Измените свойства блока queue. Введите Customer в поле Класс заявки. Добавьте код в поля:

Действие при входе: entity.startWaiting = time();

Действие при выходе:

waitTimeDistr.add(time()-entity.startWaiting);

Данный код добавляет время, в течение которого клиент ожидал обслуживания, в объект сбора данных waitTimeDistr;

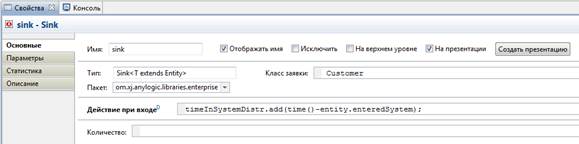
8) Измените свойства блока sink. Введите Customer в поле Класс заявки. Введите в поле Действие при входе следующий код:

timeInSystemDistr.add(time()-entity.enteredSystem) ;. Этот код добавляет полное время пребывания клиента в банковском отделении в объект сбора данных гистограммы timeInSystemDistr.

9) Запустите модель и просмотрите статистику с помощью окон инспекта (открыть окно инспекта можно, щелкнув мышью по значку Данные гистограммы). Зафиксируйте в отчете статистическую информацию для значений, собранных в данных объектах сбора статистики.

10) Добавьте гистограмму для отображения распределения времени ожидания клиента в очереди. Перетащите элемент Гистограмма из палитры Статистика. Поместите ее под элементом сбора данных (см. рис. 15). В свойствах гистограммы щелкните мышью по кнопке Добавить данные и введите в поле Данные имя соответствующего элемента – waitTimeDistr. На гистограмме будет отображаться распределение времени ожидания клиента. Измените Заголовок на Распределение времени ожидания.

11) Аналогичным образом добавьте еще одну гистограмму, расположите ее под ранее добавленной. В поле Данные введите timeInSystemDistr. На гистограмме будет отображаться распределение времени пребывания клиента в системе. Измените Заголовок на Распределение времени пребывания.

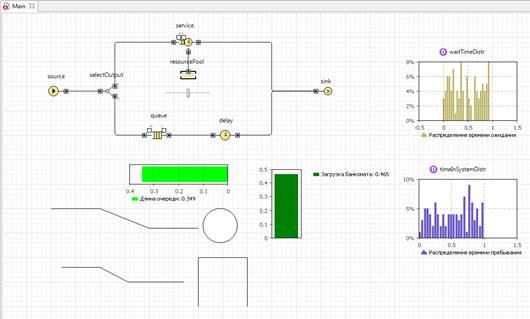
Рис. 15.

12. Запустите модель. Включите режим виртуального времени. Какой вид примет распределение времени ожидания и времени пребывания клиента в системе?

13. Внесите изменения в модель банковского отделения согласно варианту (см. табл. 1). Запустите модель. Сравните результаты прогона модели с исходными и новыми значениями входных данных. Сделайте выводы. Эффективно ли работает система с новыми значениями интенсивностей входного потока и потока обслуживания? Как изменилось среднее время ожидания клиента? Влияет ли количество кассиров на время пребывания клиента в системе?

Таблица 1.

Вари-ант	Распределение вероятности прихода клиентов в банк	Вероятность обращения к кассиру/ к банкомату	Время обслуживания клиента кассиром	Количе-ство кассиров
	Экспоненциальное	1/1	4 ± 2
	Экспоненциальное	1/2	6 ± 2
	Экспоненциальное	2/1	8 ± 2
	Экспоненциальное	1/3	7 ± 2
	Экспоненциальное	3/1	9 ± 2
	Нормальное	1/1	8 ± 2
	Нормальное	1/2	7 ± 2
	Нормальное	2/1	9 ± 2
	Нормальное	1/3	4 ± 2
	Нормальное	3/1	6 ± 2
	Треугольное	1/1	2 ± 2
	Треугольное	1/2	7 ± 2
	Треугольное	2/1	9 ± 2
	Треугольное	1/3	4 ± 2
	Треугольное	3/1	6 ± 2
	Равномерное	1/1	4 ± 2
	Равномерное	1/2	6 ± 2
	Равномерное	2/1	7 ± 2
	Равномерное	1/3	8 ± 2
	Равномерное	3/1	9 ± 2

14. Самостоятельно постройте еще одну новую модель системы массового обслуживания. (Варианты заданий приведены ниже.) Назовите модель smo 2. alp. Создайте анимацию для модели. Анимация модели должна включать следующие элементы: название и описание модели; слайдеры для задания параметров модели; графики и/или диаграммы; анимацию процесса обслуживания. Используйте закрашенные прямоугольники или встройте изображение для задания фона Вашей презентации. Настройте также две области просмотра презентации модели: область просмотра логики (схема процесса) и область просмотра анимации. (Область просмотра задается с помощью палитры Презентация.) Сравните результаты моделирования в GPSS и AnyLogic.

Варианты 1, 11

Имеется некоторая конвейерная автоматизированная линия по выпуску баночек фруктового сока.

Пустые баночки для фруктового сока поступают в накопитель 1 автоматизированной ли­нии каждые3,5 ± 1,1секунд. После этого в них автоматически заливает­ся сок. Одновременно может заливаться лишь одна баночка, на что расходуется 1,5секунды. Потом баночки поступают в накопитель 2 для выполнения операции закупоривания. Для этого расходуется 1,6секунд времени на каждую баночку. Одновременно может обраба­тываться одна баночка. Потом они попадают в накопитель 3 для следующей операции. В конце конвейера баночки устанавливаются в ящики. Время установки одной баночки представляет собой равно­мерно распределенную случайную величину в интервале 2,0 ± 0,8секунд. Одновременно может устанавливаться в ящик не боль­ше двух баночек.В начале смены в накопителе 2 находится 20баночек,ав накопителе 3 – 36баночек. Определите,какие размеры должны иметь накопители. Промодели­руйте работу линии на протяжении одной смены (8часов).

Варианты 2, 12

В состав двухпроцессорной системы входят: два процессора под символическими именами PR 1 и PR 2 и оперативная память.

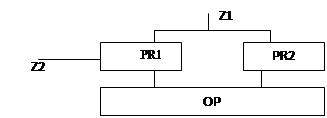
Система обрабатывает потока заявок Z 1 и Z 2, поступающих в систему по равномерному закону с интервалами 4 ± 2 и 25 ± 2 соответственно. Поток заявок Z 2 обрабатывается только на PR 1 и придерживает обработку заявок потока Z 1, после чего прерванная заявка дообслуживается. Обслуживание заявок потока Z 1 происходит по условию: если очередь PR 2 > PR 1,то обслуживание происходит на PR 1, иначе на PR 2. После обработки на процессорах заявка помещается в оперативную память. Смоделируйте систему без потерь.

Варианты 3, 13

В небольшом кафе работают две официантки (А и B)обслужи­вая по 5четырехместных столиков. Официантка А пользуется боль­шей популярностью, чем официантка В. Приходя в кафе, клиент са­дится за столик официантки В только в том случае, если все места за столиками, которые обслуживает официантка А, заняты. Клиенты приходят в кафе через 2 ± 1 минут и, если не застают свободных мест, становятся в очередь. Когда клиент садится на освободившееся место, он ждет, пока к нему подойдет официантка и примет у него заказ. Время приема зака­за у официантки А занимает 45 ± 15 секунд, у официантки В соответст­венно17 ± 4 секунд. Приняв заказ у клиента, официантки сразу же его выполняют. Время выполнения заказа обеими официантками состав­ляет 160 ± 20секунд. После получения заказа клиент на протяжении 16 ± 4минут обедает и уходит из кафе. Официантки обслуживают клиентов по принципу FIFO и в каждый момент времени могут об­служивать не более одного клиента. Определитьвремя ожидания в очереди и время, которое клиент проводит за столиком кафе. Промоделируйте работу кафе на протя­жении 10 ч.

Варианты 4, 14

В студенческом машинном зале расположены две ЭВМ и одно устройство подготовки данных (УПД). Студенты приходят с интервалом в 8 ± 2 мин, и треть из них хочет использовать УПД и ЭВМ, а остальные только ЭВМ. Допустимая очередь в машинном зале составляет четыре человека, включая работающего на УПД. Работа на УПД занимает 8 ± 1 мин, а на ЭВМ – 17 мин. Кроме того, 20% работавших на ЭВМ возвращается для повторного использования УПД и ЭВМ. Смоделируйте работу машинного зала в течение 60 ч. Определите загрузку УПД, ЭВМ и вероятность отказа в обслуживании вследствие переполнения очереди.

Варианты 5, 15

В вычислительном классе на обработку принимаются три класса заданий А, В, С. Исходя из наличия оперативной памяти ЭВМ задания классов А и В могут решаться одновременно, а задания класса С монополизируют ЭВМ. Задания класса А поступают через 20 ± 5 мин, класса В – через 20 ± 10 мин и класса С – через 30 ± 10 мин и требуют для выполнения: класс А – 20 ± 5 мин, класс В – 21 ± 3 мин и класс С – 28 ± 5 мин. Задачи класса С загружаются в ЭВМ, если она полностью свободна. Задачи класса А и В могут дозагружаться к решающей задаче. Смоделируйте процесс обслуживания в течение 80 ч. Определите загрузку ЭВМ.

Варианты 6, 16

Пять операторов работают в справочной телефонной сети города, сообщая номера телефонов по запросам абонентов, которые обращаются по одному номеру - 09. Автоматический коммутатор переключает абонента на того оператора, в очереди которого ожидает наименьшее количество абонентов, причем наибольшая допустимая длина очереди перед оператором – два абонента. Если все очереди имеют максимальную длину, вновь поступивший вызов получает отказ. Обслуживание абонентов операторами длится 30 ± 20 с. Вызовы поступают в справочную через каждые 5 ± 3 с. Смоделируйте обслуживание 200 вызовов. Подсчитайте количе­ство отказов. Определите коэффициенты загрузки операторов справочной.

Вариант 7, 17

Собранные телевизоры проходят серию испытаний на станции технического контроля. Если оказывается, что функционирование те­левизора ненормально, то отбракованный телевизор передают в цех наладки, где заменяют неисправные блоки. После наладки телевизор возвращают на станцию контроля и снова проверяют. Со станции технического контроля телевизоры после одной или нескольких про­верок поступают в цех упаковки.

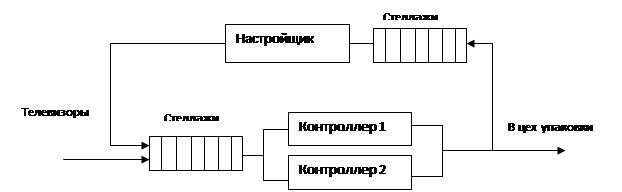
Телевизоры попадают на станцию технического контроля каж­дые 5,5 ± 2,0 минут. На станции работают 2 контролера одинаковой квалификации. Операция контроля одного телевизора состоит из двух проверок:

1) для первой проверки каждому контролеру необходимо 9± 3 минут;

2) для второй проверки на всех контролеров имеется один тес­товый прибор (продолжительность тестирования – 1,2 минут).

Приблизительно 85 процентов телевизоров успешно проходят проверку и попадают в цех упаковки, а другие 15 процентов – в цех наладки, в котором находится один рабочий – наладчик. Время на­ладки (замены) неисправных блоков распределено в соответствии c равномерным законом в интервале 30 ±7 минут. Промоделируйте функционирование станции технического контроля в течение 8 часов.

Вариант 8, 18

Информационно-поисковая библиографическая система построена на базе двух ЭВМ и имеет один терминал для ввода и вывода информации. Первая ЭВМ обеспечивает поиск научно-технической литературы (вероятность обращения к ней – 0,7), а вторая – медицинской (вероятность обращения к ней – 0,3). Пользователи обращаются к услугам системы каждые 5 ± 2 мин. Если в очереди к терминалу ожидают 10 пользователей, то вновь прибывшие пользователи получают отказ в обслуживании. Поиск информации на первой ЭВМ продолжается 6 ± 4 мин, а на второй 3 ± 2 мин. Для установления связи с нужной ЭВМ и передачи текста запроса пользователи тратят 2 ± 1 мин. Вывод результатов поиска происходит за 1 мин. Смоделируйте процесс работы системы за 8 часов.

Вариант 9, 19

Изготовление деталей определенного вида включает длительный процесс сборки, который заканчивается коротким периодом обжига в печи. Поскольку эксплуатация печи обходится очень дорого, несколько сборщиков используют одну печь, в которой одновременно можно обжигать только одну деталь. Сборщик не может начать новую сборку, пока не вытащит из печи предыдущую деталь. Таким образом, сборщик работает в таком режиме:

1) собирает следующую деталь;

2) ожидает возможности использования печи по принципу FIFO;

3) использует печь;

4) возвращается к п. 1.

Время, необходимое на выполнение различных операций: сборка – 30±5 мин.; обжиг – 8±2 мин.

Необходимо построить на GPSS модель описанного процесса. Определить оптимальное число сборщиков, использующих одну печь, т.е. такое количество, которое дает наибольшую прибыль при моделировании в течение 40 часов модельного времени. Предполагается, что в течение рабочего дня нет перерывов, а рабочими днями являются все дни (без выходных).

Варианты 10, 20

В вычислительный зал с интервалом времени 10±5 мин. Заходят пользователи, желающие произвести расчеты на ЭВМ. В зале имеется 8 ЭВМ, к одной ЭВМ подключен принтер. Время, необходимое для решения задачи и вывода результатов на печать, составляет 15±5 мин. Вывод результатов на печать не мешает проведению расчетов, время печати составляет 3±2 мин. В зал не допускается более 10 студентов. Смоделировать процесс обслуживания 100 пользователей. Подсчитать число пользователей, не нашедших свободного места в очереди. Определите среднее число пользователей в очереди, а также коэффициенты загрузки всех ЭВМ и принтера.

Вариант 21

Самолеты прибывают для посадки в район крупного аэропорта каждые 10 ± 5 мин. Если взлетно-посадочная полоса свободна, прибывший самолет получает разрешение на посадку. Если полоса занята, самолет выполняет полет по кругу и возвращается к аэропорту через каждые 4 мин. Если после пятого круга самолет не получает разрешения на посадку, он отправляется на запасной аэродром. В аэропорту через каждые 10 ± 2 мин к взлетно-посадочной полосе выруливают готовые к взлету машины и получают разрешение на взлет, если полоса свободна. Для взлета и посадки самолеты занимают полосу ровно на 2 мин. Если при свободной полосе одновременно один самолет прибывает для посадки, а другой – для взлета, полоса предостав­ляется взлетающей машине. Смоделируйте работу аэропорта в течение суток. Подсчитайте количество самолетов, которые взлетели, сели и были направлены на запасной аэродром. Определите коэффициент загрузки взлет­но-посадочной полосы.

Вариант 22

Вычислительная система состоит из трех ЭВМ. С интервалом 3 ± 1 мин в систему поступают задания, которые с вероятностями Р₁= 0,4, P₂= P₃= 0,3 адресуются одной из трех ЭВМ. Перед каждой ЭВМ имеется очередь заданий, длина которой не ограничена. После обработки задания на первой ЭВМ оно с вероятностью P₁₂ = 0,3 поступает в очередь ко второй ЭВМ и с вероятностью P₁₃ = 0,7 – в очередь к третьей ЭВМ. После обработки на второй или третьей ЭВМ задание считается выполненным. Продолжительность обработки заданий на разных ЭВМ характеризуется интервалами времени: Т₁= 7 ± 4 мин, T₂= 3 ± 1 мин, T₃=5 ± 2 мин. Смоделируйте процесс обработки 200 заданий. Определите максимальную длину каждой очереди и коэффициенты загрузки ЭВМ.